
���� ������ab��0��a+b��0���жϳ�a��b��������Ȼ��ֱ�����������Ŀ���жϣ�
��� �⣺��Ϊ��ab��0��a+b��0��
����a��0��b��0��
����a��0��b��0��$\sqrt{a}$��$\sqrt{b}$�����壬���Ԣٵı��δ���
��$\sqrt{\frac{b}{a}}$•$\sqrt{\frac{a}{b}}$=$\sqrt{\frac{b}{a}•\frac{a}{b}}$=1���ʢ���ȷ��
��$\sqrt{ab}$��$\sqrt{\frac{a}{b}}$=$\sqrt{ab��\frac{a}{b}}$=$\sqrt{ab��\frac{b}{a}}=\sqrt{{b}^{2}}$=|b|������b��0����ԭʽ=-b���ʢ���ȷ��
��$\sqrt{ab}$•$\sqrt{\frac{a}{b}}$=$\sqrt{ab•\frac{a}{b}}$=$\sqrt{{a}^{2}}$=|a|������a��0����ԭʽ=-a���ʢܼ������
�ʴ�Ϊ�ڢ�
���� ���⿼���˶��θ�ʽ�Ļ���������θ�ʽ�ij˳����㣮ע�⣺һ������ƽ��������ƽ��������������ľ���ֵ����$\sqrt{{a}^{2}}$=|a|��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��4��СԲ�������ȣ���Բ�İ뾶����СԲ��ֱ������ͼ����Ӱ���ֵ����S1���Բ�����S2�Ĵ�С��ϵΪ��������
��ͼ��4��СԲ�������ȣ���Բ�İ뾶����СԲ��ֱ������ͼ����Ӱ���ֵ����S1���Բ�����S2�Ĵ�С��ϵΪ��������| A�� | S1=S2 | B�� | S1=$\frac{1}{2}$S2 | C�� | S1=$\frac{1}{3}$S2 | D�� | S1=$\frac{1}{4}$S2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
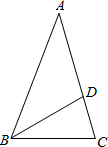 ��ͼ����֪��ABC��AB=AC=2����A=36�㣬��ABC��ƽ����BD��AC�ڵ�D����AD�ij���$\sqrt{5}$-1��
��ͼ����֪��ABC��AB=AC=2����A=36�㣬��ABC��ƽ����BD��AC�ڵ�D����AD�ij���$\sqrt{5}$-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5����1�� | B�� | 5����2�� | C�� | 4����1�� | D�� | 4����2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com