
分析 (1)先算零指数幂,负整数指数幂,平方,再计算加减法即可求解;
(2)先算积的乘方,再根据单项式的乘法法则计算即可求解;
(3)先算同底数幂的乘除法,积的乘方,再合并同类项即可求解;
(4)先根据平方差公式,完全平方公式计算,再合并同类项即可求解.
解答 解:(1)${({π-3.14})^0}+{2^{-2}}+{(-3)^2}-{(\frac{1}{2})^{-2}}$
=$1+\frac{1}{4}+9-4$
=$6\frac{1}{4}$;
(2)${(-2x{y^2})^3}•{(-3{x^2}{y^3})^2}•(\frac{1}{4}xy)$
=$-8{x^3}{y^6}•9{x^4}{y^6}•\frac{1}{4}xy$
=-18x8y13;
(3)a2•a3•a5+(-2a5)2-a12÷a2
=a10+4a10-a10
=4a10;
(4)(2x+1)(2x-1)-4(x-1)2
=4x2-1-4(x2-2x+1)
=4x2-1-4x2+8x-4
=8x-5.
点评 考查了整式的混合运算,关键是熟练掌握积的乘方,单项式的乘法,同底数幂的乘除法,合并同类项,完全平方公式,平方差公式的计算法则,同时考查了实数的运算.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
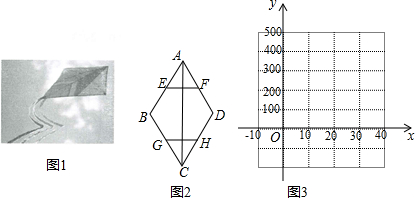
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 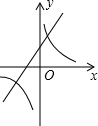 | B. | 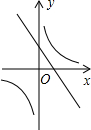 | C. |  | D. | 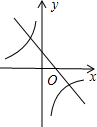 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
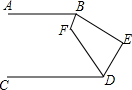 如图,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠F=125°,则∠E的度数为( )
如图,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠F=125°,则∠E的度数为( )| A. | 120° | B. | 115° | C. | 110° | D. | 105° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
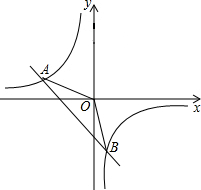 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.
已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com