
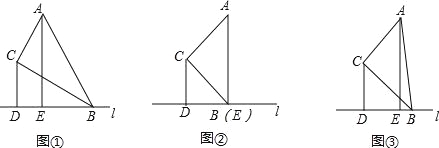
����Ŀ������ABC�У���ACB=90�㾭����B��ֱ��l��l����ֱ��AB�غϣ���ֱ��BC�ļнǵ�����ABC���ֱ����C��A��ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��D��E��
��1�����ⷢ����
������ABC=30�㣬��ͼ������![]() = ��
= ��
����ABC=45�㣬��ͼ������![]() = ��
= ��
��2����չ̽����
��0������ABC��90�㣬![]() ��ֵ���ޱ仯�������ͼ�������θ���֤����
��ֵ���ޱ仯�������ͼ�������θ���֤����
��3����������
��ֱ��CE��AB���ڵ�F��![]() =
=![]() ��CD=4����ֱ��д���߶�BD�ij���
��CD=4����ֱ��д���߶�BD�ij���
���𰸡���1����![]() ����
����![]() ����2��
����2��![]() ��ֵ�ޱ仯���������������(3) 2��8��
��ֵ�ޱ仯���������������(3) 2��8��
��������
�����������1��������ֱ�������ε����ʵõ�CD=![]() BC������ȫ�������ε����ʵõ�BC=AE�����������õ�CD=
BC������ȫ�������ε����ʵõ�BC=AE�����������õ�CD=![]() AE�����ɵõ����ۣ�����ͼ�����Ƴ���ACB�ǵ���ֱ�������Σ������CBD=45�㣬֤��B��E�غϣ����ݵ���ֱ�������ε����ʵõ�EF=
AE�����ɵõ����ۣ�����ͼ�����Ƴ���ACB�ǵ���ֱ�������Σ������CBD=45�㣬֤��B��E�غϣ����ݵ���ֱ�������ε����ʵõ�EF=![]() AE���ݾ��ε����ʵõ�EF=CD����õ����ۣ�
AE���ݾ��ε����ʵõ�EF=CD����õ����ۣ�
��2����ͼ�����ӳ�AC��ֱ��L����G�����ݵ��������ε����ʵõ�BA=BG��֤��CD��AE���������������ε����ʵõ�![]() ��
��
��3��������F���߶�AB��ʱ����C��CG��l��AE��H����AB��G���Ƴ���CFG�ס�EFB���������������ε����ʵõ�![]() ����CG=5x��BE=6x����AB=10x���ߡ����ݹ��ɶ����õ�AE=8x���ɣ�2����AE=2CD���������������ε����ʵõ�
����CG=5x��BE=6x����AB=10x���ߡ����ݹ��ɶ����õ�AE=8x���ɣ�2����AE=2CD���������������ε����ʵõ�![]() �����ǵõ�CH=CG+HG=8������ƽ���ı��ε����ʵõ�DE=CH=8�����BD=DE=BE=2������ͼ��������F���߶�BA���ӳ�����ʱ������C��CG��l��AE�ڵ�H����AB��G��ͬ���ɵ���ý��ۣ�
�����ǵõ�CH=CG+HG=8������ƽ���ı��ε����ʵõ�DE=CH=8�����BD=DE=BE=2������ͼ��������F���߶�BA���ӳ�����ʱ������C��CG��l��AE�ڵ�H����AB��G��ͬ���ɵ���ý��ۣ�
�����������1������CD��BD��
���CDB=90�㣬
�ߡ�DBC=��ABC=30�㣬
��CD=![]() BC��
BC��
����ABE����ABC��
��ACB=��AEB=90������BAE=��ABC=30����AB=BA��
���ABC�ա�ABE��
��BC=AE��
��CD=![]() AE��
AE��
��![]() =
=![]() ��
��
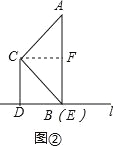
����ͼ�����ߡ�ABC=45����ACB=90�㣬
���ACB�ǵ���ֱ�������Σ�
�ߡ�CBD=45�㣬
���ABD=90�㣬
��AE��BC��
��B��E�غϣ�
��EF=![]() AE��
AE��
��CD��BD��
���ı���CDEF�ľ��Σ�
��EF=CD��
��CD=![]() AE��
AE��
��![]() =
=![]() ��
��
�ʴ�Ϊ����![]() ����
����![]() ��
��
��2��![]() ��ֵ�ޱ仯��
��ֵ�ޱ仯��
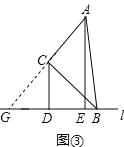
���ɣ���ͼ�����ӳ�AC��ֱ��L����G��
���ABC=��CBG��
�ߡ�ACB=90�㣬
���AGB=��BAG��
��BA=BG��
��AE��l��CD��l��
��CD��AE��
���GCD�ס�GAE��
��![]() ��
��
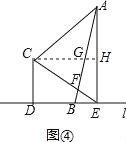
��3������ͼ4������F���߶�AB��ʱ����C��CG��l��AE��H����AB��G��
���DBC=��HCB��
�ߡ�DBC=��CBF��
���CBF=��HCB��
��CG=BG��
�ߡ�ACB=90�㣬
���CAG+��CBF=��HCB+��ACG=90�㣬
���ACG=��CAG��
��CG=AG=BG��
��CG��l��
���CFG�ס�EFB��
��![]() ��
��
��CG=5x��BE=6x��
��AB=10x��
�ߡ�AEB=90�㣬
��AE=8x��
�ɣ�2����AE=2CD��
��CD=4��
��AE=8��
��x=1��
��AB=10��BE=6��CG=5��
��GH��l��
���AGH�ס�ABE��
��![]() ��
��
��HG=3��
��CH=CG+HG=8��
��CG��l��CD��AE��
���ı���CDEHΪƽ���ı��Σ�
��DE=CH=8��
��BD=DE=BE=2��
����ͼ��������F���߶�BA���ӳ�����ʱ������C��CG��l��AE�ڵ�H����AB��G��
ͬ���ɵ�CG=5��BH=6��HG=3��
��DE=CH=CG��HG=2��
��BD=DE+BE=8��
���Ͽɵ�BD=2��8��



 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� Ŀ�����ϵ�д�
Ŀ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AC,��A=36�㣬AB���д���MN��AC�ڵ�D,��AB�ڵ�M,
��֤����1��BDƽ�֡�ABC��
��2����BCD����������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
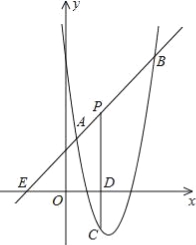
����Ŀ����ͼ��ֱ��y=x+2��������y=![]() +bx+6��a��0���ཻ��A��
+bx+6��a��0���ཻ��A��![]() ��
��![]() ����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
��1���������ߵĽ���ʽ��
��2���Ƿ����������P�㣬ʹ�߶�PC�ij������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��3������PACΪֱ��������ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и������У�������Ϊֱ�����������߳����ǣ�������
A. 1.5��2��3 B. 5��12��13 C. 7��24��25 D. 8��15��17
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ı��ε��ܳ���48���ף���֪��һ���߳�a���ף��ڶ����߱ȵ�һ���ߵ�2����3���ף��������ߵ��ڵ�һ���������ߵĺͣ�д����ʾ�������߳�����ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ODƽ�֡�BOC��OEƽ�֡�AOC������BOC=70�㣬��AOC=50�㣮
��1�������AOB���䲹�ǵĶ�����
��2���������DOC�͡�AOE�Ķ��������жϡ�DOE���AOB�Ƿ�����˵�����ɣ�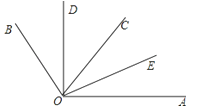
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������Ź�80�ˣ����ű�����������2����5�ˣ��������Ÿ��ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����DΪBC��һ�㣬��AD=DC����A��B��D��������O��AE����O��ֱ��������DE��
��1����֤��AC����O�����ߣ�
��2����sinC=![]() ��AC=6������O��ֱ����
��AC=6������O��ֱ����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com