
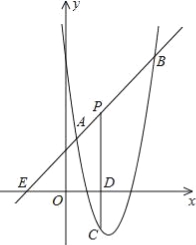
【题目】如图,直线y=x+2与抛物线y=![]() +bx+6(a≠0)相交于A(
+bx+6(a≠0)相交于A(![]() ,
,![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
【答案】(1) y=![]() ﹣8x+6;(2) 当n=
﹣8x+6;(2) 当n=![]() 时,线段PC最大值为
时,线段PC最大值为![]() ;(3) (3,5)或(
;(3) (3,5)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.
(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.
(3)当△PAC为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.
试题解析:(1)∵B(4,m)在直线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A(![]() ,
,![]() )、B(4,6)在抛物线y=
)、B(4,6)在抛物线y=![]() +bx+6上,
+bx+6上,
∴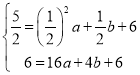 ,解得
,解得![]() ,
,
∴抛物线的解析式为y=![]() ﹣8x+6;
﹣8x+6;
(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,![]() ﹣8n+6),
﹣8n+6),
∴PC=(n+2)﹣(![]() ﹣8n+6),
﹣8n+6),
=﹣![]() +9n﹣4,
+9n﹣4,
=![]() ,
,
∵PC>0,
∴当n=![]() 时,线段PC最大值为
时,线段PC最大值为![]() ;
;
(3)∵△PAC为直角三角形,
i)若点P为直角顶点,则∠APC=90°.
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
ii)若点A为直角顶点,则∠PAC=90°.
如答图3﹣1,过点A(![]() ,
,![]() )作AN⊥x轴于点N,则ON=
)作AN⊥x轴于点N,则ON=![]() ,AN=
,AN=![]() .
.
过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,
∴MN=AN=![]() ,∴OM=ON+MN=
,∴OM=ON+MN=![]() +
+![]() =3,
=3,
∴M(3,0).
设直线AM的解析式为:y=kx+b,
则: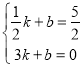 ,解得
,解得![]() ,
,
∴直线AM的解析式为:y=﹣x+3①,
又抛物线的解析式为:y=![]() ﹣8x+6②,
﹣8x+6②,
联立①②式,解得:x=3或x=![]() (与点A重合,舍去),
(与点A重合,舍去),
∴C(3,0),即点C、M点重合.
当x=3时,y=x+2=5,
∴![]() (3,5);
(3,5);
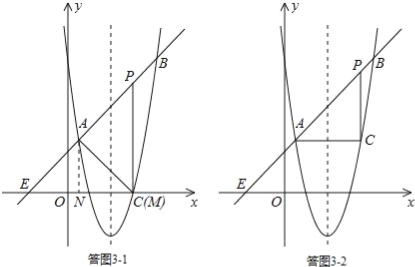
iii)若点C为直角顶点,则∠ACP=90°.
∵y=![]() ﹣8x+6=
﹣8x+6=![]() ,
,
∴抛物线的对称轴为直线x=2.
如答图3﹣2,作点A(![]() ,
,![]() )关于对称轴x=2的对称点C,
)关于对称轴x=2的对称点C,
则点C在抛物线上,且C(![]() ,
,![]() ).
).
当x=![]() 时,y=x+2=
时,y=x+2=![]() .
.
∴![]() (
(![]() ,
,![]() ).
).
∵点![]() (3,5)、
(3,5)、![]() (
(![]() ,
,![]() )均在线段AB上,
)均在线段AB上,
∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
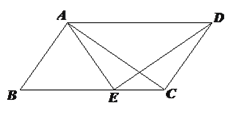
【题目】如图,在四边形ABCD中,AB//CD,∠B=∠ADC,点E是BC边上的一点,且AE=DC.
(1)求证:△ABC≌△EAD ;
(2)如果AB⊥AC,求证:∠BAE= 2∠ACB.
查看答案和解析>>
科目:初中数学 来源: 题型:
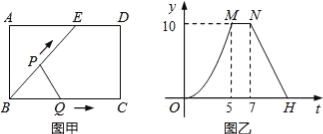
【题目】如图甲,点E为矩形ABCD边AD上一点,点P,Q同时从B点出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为y(![]() ),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论:
),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论:
①当0<t≤5时,y=![]() ;②tan∠ABE=
;②tan∠ABE=![]() ;③点H的坐标为(11,0);④△ABE与△QBP不可能相似.
;③点H的坐标为(11,0);④△ABE与△QBP不可能相似.
其中正确的是 (把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=37°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周老师在一次“探究性学习”课中,设计了如下数表:

(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=__ _____;b=___ ____;c=___ ____;
(2)猜想:以a,b,c为边长的三角形是否是直角三角形?证明你的猜想.
(3)、显然,满足这样关系的整数a、b、c我们把它叫做 数,请再写一组这样的数 (不同于表格中已出现的数组)
查看答案和解析>>
科目:初中数学 来源: 题型:
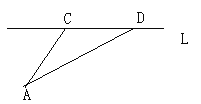
【题目】如图,某公司(A点)与公路(直线L)的距离为300米,又与公路车站(D点)的距离为500米,现要在公路边建一个物流站(C点),使之与该公司A及车站D的距离相等,求物流站与车站之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
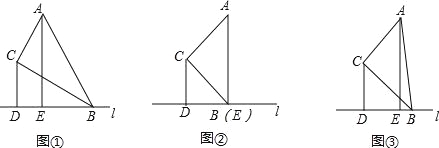
【题目】在△ABC中,∠ACB=90°经过点B的直线l(l不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、A做直线l的垂线,垂足分别为点D、E.
(1)问题发现:
①若∠ABC=30°,如图①,则![]() = ;
= ;
②∠ABC=45°,如图②,则![]() = ;
= ;
(2)拓展探究:
当0°<∠ABC<90°,![]() 的值有无变化?请仅就图③的情形给出证明.
的值有无变化?请仅就图③的情形给出证明.
(3)问题解决:
若直线CE、AB交于点F,![]() =
=![]() ,CD=4,请直接写出线段BD的长.
,CD=4,请直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”期间,某商店将单价标为130元的书包按8折出售可获利30%,该书包每个的进价是( )
A. 65元 B. 80元 C. 100元 D. 104元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com