
����Ŀ����ͼ��MN��ʾһ�α�ֱ�ĸܵ�·���߶�AB��ʾ�ܵ�·�Ե�һ�ž���¥����֪��A��MN�ľ���Ϊ15�ף�BA���ӳ�����MN�ཻ�ڵ�D������BDN=37�㣬���������ڸ��ٵ�·����ʻʱ����Χ39�����ڻ��ܵ�������Ӱ�죮
��1������A��MN�Ĵ��ߣ�����Ϊ��H������������Ŵ�M��N�ķ�����MN����ʻ�������������P��ʱ��������ʼӰ����һ�ŵľ���¥����ô��ʱ�������H�ľ���Ϊ�����ף�
��2������������һ�ַ������ڸܵ�·��װ�����壬��������ʻ����Qʱ��������һ�ž���¥�ľ���QCΪ39�ף���ô������һ�ž���¥���ܵ�·��װ�ĸ�����������Ҫ�����׳������ο����ݣ�sin37��=0.60��cos37��=0.80��tan37��=0.75��

���𰸡�(1) 36�ף�(2) 81�ף�
��������
�����������1������PA����ֱ����PAH�����ù��ɶ�������PH�ij��ȣ�
��2��������֪��������ij�����PQ�ij��ȣ�ͨ����Rt��ADH��Rt��CDQ�ֱ����DH��DQ�ij��ȣ�Ȼ����ͼ�εõ���PQ=PH+DQ��DH��������߶εij��ȴ�����ֵ���ɣ�
�����������1����ͼ������PA��
������֪��AP=39m��
��ֱ����APH�У�PH=![]() =
=![]() =36���ף���
=36���ף���
�𣺴�ʱ�������H�ľ���Ϊ36�ף�
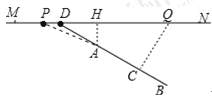
��2��������֪��������ij�����PQ�ij��ȣ�
��Rt��ADH�У�DH=![]() =20���ף���
=20���ף���
��Rt��CDQ�У�DQ=![]() =65���ף���
=65���ף���
��PQ=PH+HQ=PH+DQ��DH=36+65��20=81���ף���
�𣺸ܵ�·��װ�ĸ�����������Ҫ81�ף�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪��������һ�����������������ĺ�Ϊ������������һ����Ϊ�����������һ���������Ļ�Ϊ���������������������Ļ�Ϊ�㣮�ɴ˿ɵã����ax+b=0������a��bΪ��������xΪ����������ôa=0��b=0��
��������֪ʶ������������⣺
��1�������a-2��![]() +b+3=0������a��bΪ����������ôa= ��b= ��
+b+3=0������a��bΪ����������ôa= ��b= ��
��2�������2+![]() ��a-��1-
��a-��1-![]() ��b=5������a��bΪ����������a+2b��ֵ��
��b=5������a��bΪ����������a+2b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦΪ�˰����༶���ͥ���ѵ�x�����ӣ�x��10����������һ�������飬�����ÿ����ͥ���ѵĺ��ӷ�5������ôʣ��4���������ÿ����ͥ���ѵĺ��ӷ�6������ô���һ������ֻ�ܵõ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣨3a2��2a��1������2a2��3a��5���Ľ���ǣ� ��
A. a2��5a��6 B. 7a2��5a��4 C. a2��a��4 D. a2��a��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��x2����ƽ��2����λ��������ƽ��5����λ����ƽ�ƺ������������ߵı���ʽΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
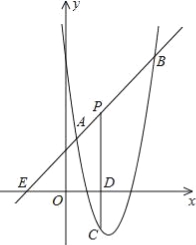
����Ŀ����ͼ��ֱ��y=x+2��������y=![]() +bx+6��a��0���ཻ��A��
+bx+6��a��0���ཻ��A��![]() ��
��![]() ����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
��1���������ߵĽ���ʽ��
��2���Ƿ����������P�㣬ʹ�߶�PC�ij������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��3������PACΪֱ��������ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij����װ����һ���ݵ����A��һ�������ij���B��
�±���С������һЩ�������õĽ����
A | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
B | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 |
��1�������������5����С����������Ƕ��٣�
��2����С�����������225��������Ľ���Ƕ��٣�
��3����С�����������n��n��10���������ú�n��ʽ�ӱ�ʾ����Ľ������һ�ԣ�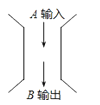
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ı��ε��ܳ���48���ף���֪��һ���߳�a���ף��ڶ����߱ȵ�һ���ߵ�2����3���ף��������ߵ��ڵ�һ���������ߵĺͣ�д����ʾ�������߳�����ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com