
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,交抛物线于点
,交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.


(1)求抛物线的函数表达式及点![]() 、点
、点![]() 的坐标;
的坐标;
(2)抛物线对称轴上的一动点![]() 从点
从点![]() 出发,以每秒1个单位的速度向上运动,连接
出发,以每秒1个单位的速度向上运动,连接![]() ,
,![]() ,设运动时间为
,设运动时间为![]() 秒(
秒(![]() ),在点
),在点![]() 的运动过程中,请求出:当
的运动过程中,请求出:当![]() 为何值时,
为何值时,![]() ?
?
(3)若点![]() 在抛物线上
在抛物线上![]() 、
、![]() 两点之间运动(点
两点之间运动(点![]() 不与点
不与点![]() 、
、![]() 重合),在运动过程中,设点
重合),在运动过程中,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求
的函数关系式,并求![]() 为何值时
为何值时![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() =
=![]() ;(3)
;(3)![]() ,当
,当![]() 为
为![]() 时
时![]() 有最大值,最大值是
有最大值,最大值是![]() .
.
【解析】
(1)根据对称轴和A点坐标可确定B点坐标,然后将A、B坐标代入抛物线求出a,b的值,即可得到解析式,然后将![]() 代入解析式,即可求出D坐标;
代入解析式,即可求出D坐标;
(2)![]() 秒时,点
秒时,点![]() ,先利用两点间的距离公式表示出
,先利用两点间的距离公式表示出![]() ,
,![]() ,
,![]() ,再根据勾股定理建立方程求解;
,再根据勾股定理建立方程求解;
(3)作直线![]() 轴于点
轴于点![]() ,交
,交![]() 于
于![]() ,首先求直线BC解析式,用t表示出Q和G的坐标,得出QG的长度,然后利用三角形面积公式得到S与t的函数关系式,再根据二次函数的性质求最值即可.
,首先求直线BC解析式,用t表示出Q和G的坐标,得出QG的长度,然后利用三角形面积公式得到S与t的函数关系式,再根据二次函数的性质求最值即可.
(1)∵抛物线![]() 与
与![]() 轴交于
轴交于![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,
,
∴点![]() .
.
将![]() ,
,![]() 代入抛物线
代入抛物线![]() 中,
中,
得![]() ,解得
,解得![]()
![]() 抛物线的表达式为:
抛物线的表达式为:![]()
抛物线的对称轴为![]() ,
,
当![]() 时,
时,![]()
∴点![]() .
.
(2)如图,

![]() 秒时,点
秒时,点![]() ,
,
![]() ,
,![]() ,
,![]()
∵![]()
∴![]() ,
,
即![]() ,整理得
,整理得![]()
解得:![]() (舍去)
(舍去)
所以当![]() =
=![]() 时,
时,![]() ;
;
(3)如图,作直线![]() 轴于点
轴于点![]() ,交
,交![]() 于
于![]() .
.

将![]() 代入
代入![]() ,得
,得![]()
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
由![]() 两点的坐标得
两点的坐标得![]() ,解得
,解得![]()
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() ,
,
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
![]()
![]()
![]()
∵![]() ,
,
![]() 有最大值,当
有最大值,当![]() 时,
时,![]() 最大
最大![]()
综上,![]() 与
与![]() 的函数表达式为
的函数表达式为![]() ,当
,当![]() 为
为![]() 时
时![]() 有最大值,最大值是
有最大值,最大值是![]() .
.


科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
| … | -4 | -3 | -2 | -1 | 0 | … |
| … | -5 | 0 | 3 | 4 | 3 | … |
(1)求此二次函数的表达式;
(2)画出此函数图象(不用列表).
(3)结合函数图象,当-4<x≤1时,写出y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,二次函数y=x2﹣2mx+m2+2m+2的图象与x轴有两个交点.
(1)当m=﹣2时,求二次函数的图象与x轴交点的坐标;
(2)过点P(0,m﹣1)作直线1⊥y轴,二次函数图象的顶点A在直线l与x轴之间(不包含点A在直线l上),求m的范围;
(3)在(2)的条件下,设二次函数图象的对称轴与直线l相交于点B,求△ABO的面积最大时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() ,
,![]() 是
是![]() 的边
的边![]() 上一点.
上一点.

(1)将![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,请在网格中画出
,请在网格中画出![]() ;
;
(2)将![]() 沿一定的方向平移后,点
沿一定的方向平移后,点![]() 的对应点为
的对应点为![]() ,请在网格中画出上述平移后的
,请在网格中画出上述平移后的![]() ,并写出点
,并写出点![]() 的坐标:
的坐标:![]() ( );
( );
(3)若以点![]() 为位似中心,作
为位似中心,作![]() 与
与![]() 成
成![]() 的位似,则与点
的位似,则与点![]() 对应的点
对应的点![]() 位似坐标为______(不用作图,直接写出结果).
位似坐标为______(不用作图,直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织首届“数学文化节”活动,旨在引导同学们感受数学魅力,提升数学素养,活动中,九年级全体同学参加了“趣味数学知识竞赛”.活动中获得“数学之星”称号的小颖得到了![]() 四枚纪念章,(除头像外完全相同),如图所示,四枚纪念章上分别印有四位数学家的头像,她将纪念章背面朝上放在桌面上,然后从中随机选取两枚送给妹妹,求小颖送给妹妹的两枚纪念章中恰好有一枚印有华罗庚头像的概率.(提示:答题时可用序号
四枚纪念章,(除头像外完全相同),如图所示,四枚纪念章上分别印有四位数学家的头像,她将纪念章背面朝上放在桌面上,然后从中随机选取两枚送给妹妹,求小颖送给妹妹的两枚纪念章中恰好有一枚印有华罗庚头像的概率.(提示:答题时可用序号![]() 表示相应的纪念章)
表示相应的纪念章)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.

(1)如图1、用含x的代数式表示△MNP的面积S;
(2)如图2、⊙O与直线BC相切D点,求x的值为多少?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,顶点O(0,0),A(﹣3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O逆时针旋转,每次旋转90°,则第2019次旋转结束时,点D的坐标为( )
A.(3,﹣10)B.(10,3)C.(﹣10,﹣3)D.(10,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生的环保意识,某校组织了一次全校2000名学生都参加的“环保知识”考试,考题共10题.考试结束后,学校团委随机抽查部分考生的考卷,对考生答题情况进行分析统计,发现所抽查的考卷中答对题量最少为6题,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题: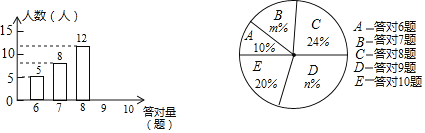
(1)本次抽查的样本容量是 ;在扇形统计图中,m= ,n= ,“答对8题”所对应扇形的圆心角为 度;
(2)将条形统计图补充完整;
(3)请根据以上调查结果,估算出该校答对不少于8题的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 矩形
矩形![]() ,连结
,连结![]() ,延长
,延长![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,延长
,延长![]() 、
、![]() 交于点
交于点![]() ,一定能求出
,一定能求出![]() 面积的条件是( )
面积的条件是( )
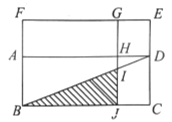
A.矩形![]() 和矩形
和矩形![]() 的面积之差B.矩形
的面积之差B.矩形![]() 和矩形
和矩形![]() 的面积之差
的面积之差
C.矩形![]() 和矩形
和矩形![]() 的面积之差D.矩形
的面积之差D.矩形![]() 和矩形
和矩形![]() 的面积之差
的面积之差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com