
【题目】平面直角坐标系xOy中,二次函数y=x2﹣2mx+m2+2m+2的图象与x轴有两个交点.
(1)当m=﹣2时,求二次函数的图象与x轴交点的坐标;
(2)过点P(0,m﹣1)作直线1⊥y轴,二次函数图象的顶点A在直线l与x轴之间(不包含点A在直线l上),求m的范围;
(3)在(2)的条件下,设二次函数图象的对称轴与直线l相交于点B,求△ABO的面积最大时m的值.
【答案】(1)抛物线与x轴交点坐标为:(﹣2+![]() ,0)(﹣2﹣
,0)(﹣2﹣![]() ,0)(2)﹣3<m<﹣1(3)当m=﹣
,0)(2)﹣3<m<﹣1(3)当m=﹣![]() 时,S最大=
时,S最大=![]()
【解析】(1)与x轴相交令y=0,解一元二次方程求解;
(2)应用配方法得到顶点A坐标,讨论点A与直线l以及x轴之间位置关系,确定m取值范围.
(3)在(2)的基础上表示△ABO的面积,根据二次函数性质求m.
(1)当m=﹣2时,抛物线解析式为:y=x2+4x+2
令y=0,则x2+4x+2=0
解得x1=﹣2+![]() ,x2=﹣2﹣
,x2=﹣2﹣![]()
抛物线与x轴交点坐标为:(﹣2+![]() ,0)(﹣2﹣
,0)(﹣2﹣![]() ,0)
,0)
(2)∵y=x2﹣2mx+m2+2m+2=(x﹣m)2+2m+2
∴抛物线顶点坐标为A(m,2m+2)
∵二次函数图象的顶点A在直线l与x轴之间(不包含点A在直线l上)
∴当直线1在x轴上方时><
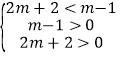
不等式无解
当直线1在x轴下方时
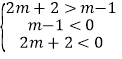
解得﹣3<m<﹣1
(3)由(1)
点A在点B上方,则AB=(2m+2)﹣(m﹣1)=m+3
△ABO的面积S=![]() (m+3)(﹣m)=﹣
(m+3)(﹣m)=﹣![]()
∵﹣![]() <0
<0
∴当m=﹣![]() 时,S最大=
时,S最大=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某花农培育甲种花木10株,乙种花木8株,共需成本6400元;培育甲种花木4株,乙种花木5株,共需成本3100元。
(1)求甲乙两种花木成本分别是多少元?
(2)若1株甲种花木售价为700元,一株乙种花木售价为500元。该花农决定在成本不超过29000元的情况下培育甲乙两种花木,若培育乙种花木的株数是甲种花木的3倍还多10株,那么要是总利润不少于18200元,花农有哪几种具体的培育方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )

A. ①②③ B. ①③④ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【操作发现】
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B= .
【问题解决】
如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
【灵活运用】
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某软件科技公司20人负责研发与维护游戏、网购、视频和送餐共4款软件.投入市场后,游戏软件的利润占这4款软件总利润的40%.如图是这4款软件研发与维护人数的扇形统计图和利润的条形统计图.
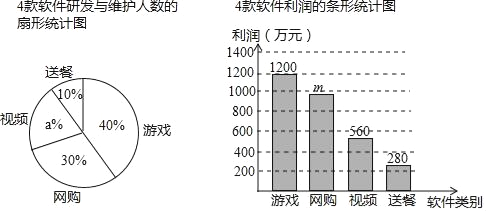
根据以上信息,网答下列问题
(1)直接写出图中a,m的值;
(2)分别求网购与视频软件的人均利润;
(3)在总人数和各款软件人均利润都保持不变的情况下,能否只调整网购与视频软件的研发与维护人数,使总利润增加60万元?如果能,写出调整方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=2,动点P从点B出发,以每秒1个单位的速度在正方形的边上沿BC-CD-DA运动,设运动时间为t,△PAB面积为S.

(1)求S关于t的函数解析式,并写出自变量t的取值范围;
(2)画出相应函数图象;
(3)当S=![]() 时,t的值为多少.
时,t的值为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电力维修小组从![]() 点出发,在东西线路上检修电线,如果规定向东为正,向西为负,一天中行驶里程(单位:千米)记录如下:+5,-4,-7,+8,-9,+6,+5
点出发,在东西线路上检修电线,如果规定向东为正,向西为负,一天中行驶里程(单位:千米)记录如下:+5,-4,-7,+8,-9,+6,+5
(1)求收工时在![]() 地的什么方位?
地的什么方位?
(2)在记录中,距离![]() 最远有 千米?
最远有 千米?
(3)若每千米耗油0.2升,油价为5元/升,问出发到收工时共需要多少元油钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com