【题目】某花农培育甲种花木10株，乙种花木8株，共需成本6400元；培育甲种花木4株，乙种花木5株，共需成本3100元。
（1）求甲乙两种花木成本分别是多少元？
（2）若1株甲种花木售价为700元，一株乙种花木售价为500元。该花农决定在成本不超过29000元的情况下培育甲乙两种花木，若培育乙种花木的株数是甲种花木的3倍还多10株，那么要是总利润不少于18200元，花农有哪几种具体的培育方案？
【答案】（1）甲、乙两种花木的成本价分别为400元和300元；（2）有三种具体方案：①种植甲种花木18株，种植乙种花木3a+10=64株；②种植甲种花木19株，种植乙种花木3a+10=67株；③种植甲种花木20株，种植乙种花木3a+10=70株．
【解析】
（1）由题意设甲、乙两种花木的成本价分别为x元和y元，并根据题干等量关系建立方程组解出方程组即可；
（2）由题意设种植甲种花木为a株，则种植乙种花木为（3a+10）株，并根据题干不等量关系建立不等式组求解即可.
解：(1)设甲、乙两种花木的成本价分别为x元和y元．
由题意得： 
，
解得： 
．
答：甲乙两种花木成本分别是400和300元.
(2)设种植甲种花木为a株，则种植乙种花木为（3a+10）株．
则有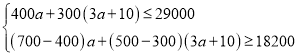
解得： 18≤a≤20，
由于a为整数，
∴a可取18或19或20.
所以有三种具体方案：
①种植甲种花木18株，种植乙种花木3a+10=64株；
②种植甲种花木19株，种植乙种花木3a+10=67株；
③种植甲种花木20株，种植乙种花木3a+10=70株．
科目：初中数学 来源： 题型：
【题目】“节能环保”是对美好家园的一种守护，某汽车制造厂生产一种新型能源汽车，计划半年后每月生产汽车20辆，由于另有任务，每月上班人数不一定相等，实际每月生产量与计划量相比情况如下表（增加为正，减少为负）：
月份 | 一 | 二 | 三 | 四 | 五 | 六 |
增减（辆） | +3 | -2 | -1 | +4 | +2 | -5 |
（1）生产量最多的一个月，比生产量最少的一个月多生产多少辆？
（2）半年内总生产量是多少？比计划多了还是少了？多或少多少辆？
查看答案和解析>>
科目：初中数学 来源： 题型：
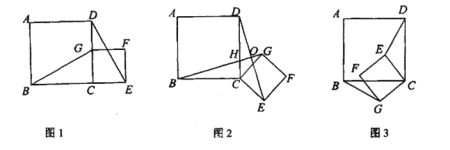
【题目】如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．(正方形四条边都相等，四个角都是直角)
1.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：
(1)猜想图1中线段BG和线段DE的长度和位置关系：______________．
(2)将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度a，得到如图2.如图3情形．请你通过观察、测量等方法判断上述猜想是否仍然成立：_______（成立、不成立）若成立，请你选取图2或图3中的一种情况说明你的判断．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点
，
在数轴上分别表示有理数
，
．
（1）对照数轴填写下表：
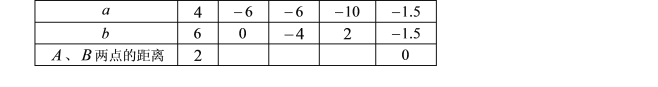
（2）若，两点间的距离记为
，试问和，
有何数量关系；
（3）写出数轴上到
和
的距离之和为
的所有整数；
（4）若
表示一个有理数，求
的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AE是∠BAC的角平分线，交BC于点E，DE∥AB交AC于点D．
(1)求证AD=ED；
(2)若AC=AB，DE=3，求AC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
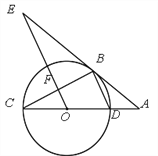
【题目】如图，CD为⊙O的直径，点B在⊙O上，连接BC、BD，过点B的切线AE与CD的延长线交于点A， 
，OE交BC于点F.
（1）求证：OE∥BD；
（2）当⊙O的半径为5， 
时，求EF的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
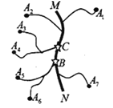
【题目】如图,在公路 MN 两侧分别有 A
, A
......A
,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是（ ）.
①车站的位置设在 C 点好于 B 点;
②车站的位置设在 B 点与 C 点之问公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关.
A.①B.②C.①③D.②③
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F．
（1）求证：四边形BEDF是平行四边形；
（2）当∠ABE为多少度时，四边形BEDF是菱形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】平面直角坐标系xOy中，二次函数y=x2﹣2mx+m2+2m+2的图象与x轴有两个交点．
（1）当m=﹣2时，求二次函数的图象与x轴交点的坐标；
（2）过点P（0，m﹣1）作直线1⊥y轴，二次函数图象的顶点A在直线l与x轴之间（不包含点A在直线l上），求m的范围；
（3）在（2）的条件下，设二次函数图象的对称轴与直线l相交于点B，求△ABO的面积最大时m的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
