练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知点，在数轴上分别表示有理数，．

    （1）对照数轴填写下表：

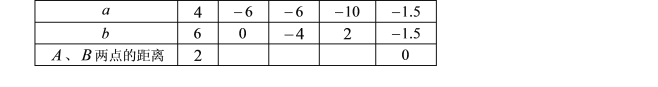
    （2）若，两点间的距离记为，试问和，有何数量关系；

    （3）写出数轴上到和的距离之和为的所有整数；

    （4）若表示一个有理数，求的最小值．

    【答案】（1），，；（2）；（3），，；（4）4

    【解析】

    (1)用数轴右侧的点减去左侧的点，即可确定两点间的距离，以此类推，填写表格即可；

    （2）根据数轴上的距离与两点间的横坐标关系解答即可；

    （3）根据（2）的关系解答即可；

    （4）根据数轴确定到1和-3距离之和的最小值即可.

    解：（1）0-（-6）=6，-4-（-6）=2，2-（-10）=12，

    故答案自左向右答案依次为：6,2,12；

    （2）根据数轴可得：和，有何数量关系为：d=b-a

    （3）根据数轴可得：到和的距离之和为的所有整数为，，；

    （4）∵-3到1的距离是1-（-3）=4，

    在-3到1之间时，取得的值最小，最小值是4

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：A（0，1），B（2，0），C（4，3）

    （1）在直角坐标系中描出各点，画出△ABC．

    （2）求△ABC的面积；

    （3）设点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有这样一个问题：探究函数的图象与性质.小彤根据学习函数的经验，对函数的图象与性质进行了探究.下面是小彤探究的过程，请补充完整：

    x

    -4

    -3.5

    -3

    -2

    -1

    0

    1

    2

    3

    3.5

    4

    y

    0

    m

    （1）求m的值为 ；

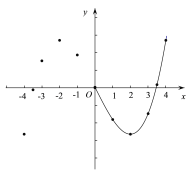
    （2）如图，在平面直角坐标系x0y 中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出了图象的一部分，请根据剩余的点补全此函数的图象；

    （3）方程实数根的个数为 ；

    （4）观察图象，写出该函数的一条性质 ；

    （5）在第（2）问的平面直角坐标系中画出直线，根据图象写出方程的一个正数根约为 （精确到0.1）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

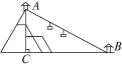
    【题目】（1）喜欢爬山的同学都知道,很多名山上都有便于游人观光的索道,如图所示,山的高度AC为800 m,从山上A与山下B处各建一索道口,且BC=1 500 m,一游客从山下索道口坐缆车到山顶,知缆车每分钟走50 m,那么大约多长时间后该游客才能到达山顶?说明理由.

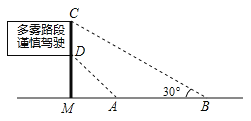
    （2）如图，是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，求警示牌的高度CD（结果精确到0.1米，参考数据：≈1.41，≈1.73）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义一种对正整数n的“F”运算：①当n为奇数时，F（n）=3n+1；②当n为偶数时，F（n）=（其中k是使F（n）为奇数的正整数）……，两种运算交替重复进行，例如，取n=24，则：

    若n=13，则第2018次“F”运算的结果是（　　）

    A. 1 B. 4 C. 2018 D. 42018

    查看答案和解析>>

    科目：初中数学 来源： 题型：

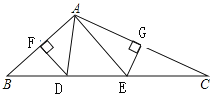
    【题目】如图,△ABC中,AB,AC边的垂直平分线分别交BC于点D,E,垂足分别为点F,G,△ADE的周长为6cm

    (1)求△ABC中BC边的长度;(2)若∠B+∠C=64°,求∠DAE的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某花农培育甲种花木10株，乙种花木8株，共需成本6400元；培育甲种花木4株，乙种花木5株，共需成本3100元。

    （1）求甲乙两种花木成本分别是多少元？

    （2）若1株甲种花木售价为700元，一株乙种花木售价为500元。该花农决定在成本不超过29000元的情况下培育甲乙两种花木，若培育乙种花木的株数是甲种花木的3倍还多10株，那么要是总利润不少于18200元，花农有哪几种具体的培育方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下表：我们把表格中字母的和所得的多项式称为“有特征多项式”，例如：

    第1格的“有特征多项式”为，，

    第2格的“有特征多项式”为，，

    回答下列问题：

    （1）第3格“有特征多项式”为__________第4格的“有特征多项式”为____________

    第格的“有特征多项式”为__________．

    （2）若第格的“特征多项式”与多项式的和不含有项，求此“有特征多项式”．

    序号

    1

    2

    3

    4

    ……

    图形

    ……

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【操作发现】

    如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．

    （1）请按要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′；

    （2）在（1）所画图形中，∠AB′B=　 　．

    【问题解决】

    如图②，在等边三角形ABC中，AC=7，点P在△ABC内，且∠APC=90°，∠BPC=120°，求△APC的面积．

    小明同学通过观察、分析、思考，对上述问题形成了如下想法：

    想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连接PP′，寻找PA，PB，PC三条线段之间的数量关系；

    想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，连接PP′，寻找PA，PB，PC三条线段之间的数量关系．

    …

    请参考小明同学的想法，完成该问题的解答过程．（一种方法即可）

    【灵活运用】

    如图③，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE=∠ADC，BE=CE=2，CD=5，AD=kAB（k为常数），求BD的长（用含k的式子表示）．

    查看答案和解析>>

    同步练习册答案