
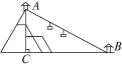
【题目】(1)喜欢爬山的同学都知道,很多名山上都有便于游人观光的索道,如图所示,山的高度AC为800 m,从山上A与山下B处各建一索道口,且BC=1 500 m,一游客从山下索道口坐缆车到山顶,知缆车每分钟走50 m,那么大约多长时间后该游客才能到达山顶?说明理由.
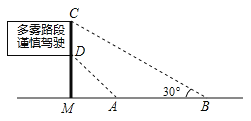
(2)如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,求警示牌的高度CD(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).
【答案】(1)34分钟;(2)CD约为2.9米.
【解析】
(1)在直角△ABC中,根据勾股定理求出AB的长,再根据路程、速度和时间的关系即可求得结果;
(2)由题意易得MA=MD=4(米),BM=4+8=12(米),根据直角三角形中30°角的性质可得CM和CB的关系,然后在直角△BMC中根据勾股定理求出CM的长,问题即得解决.
解:(1)在Rt△ABC中,根据勾股定理得:![]() (米),1700÷50=34(分钟),所以大约34分钟后该游客才能到达山顶;
(米),1700÷50=34(分钟),所以大约34分钟后该游客才能到达山顶;
(2)由题意得,△AMD和△BMC都是直角三角形,
∵∠MAD=45°,∴∠ADM=45°,∴MA=MD=4(米),
在Rt△BMC中,BM=4+8=12(米),
∵∠MBC=30°,∴BC=2MC,
设MC=x,则BC=2x,
∵![]() ,
,
∴![]() ,
,
解得![]() ,即
,即![]() (米),
(米),
∴![]() (米).
(米).
所以警示牌CD的高度约为2.9米.


科目:初中数学 来源: 题型:
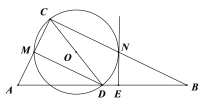
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC相交于点M、N.
(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;
(2)连接MD,求证:MD=NB.
查看答案和解析>>
科目:初中数学 来源: 题型:
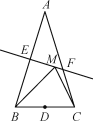
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
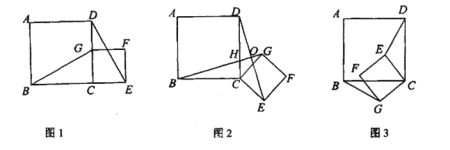
【题目】如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.(正方形四条边都相等,四个角都是直角)
1.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)猜想图1中线段BG和线段DE的长度和位置关系:______________.
(2)将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度a,得到如图2.如图3情形.请你通过观察、测量等方法判断上述猜想是否仍然成立:_______(成立、不成立)若成立,请你选取图2或图3中的一种情况说明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
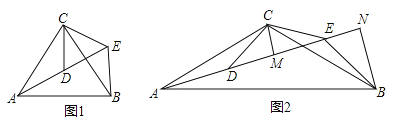
【题目】(2016山东省菏泽市)如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=![]() CM+
CM+![]() BN.
BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() .
.

(1)对照数轴填写下表:
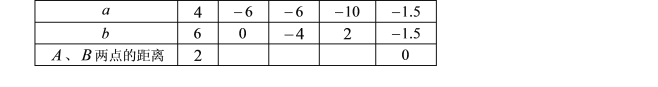
(2)若![]() ,
,![]() 两点间的距离记为
两点间的距离记为![]() ,试问
,试问![]() 和
和![]() ,
,![]() 有何数量关系;
有何数量关系;
(3)写出数轴上到![]() 和
和![]() 的距离之和为
的距离之和为![]() 的所有整数;
的所有整数;
(4)若![]() 表示一个有理数,求
表示一个有理数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
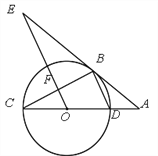
【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A, ![]() ,OE交BC于点F.
,OE交BC于点F.
(1)求证:OE∥BD;
(2)当⊙O的半径为5, ![]() 时,求EF的长.
时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国很多地区持续出现雾霾天气.某社区为了调查本社区居民对雾霾天气主要成因的认识情况,随机对该社区部分居民进行了问卷调查,要求居民从五个主要成因中只选择其中的一项,被调查居民都按要求填写了问卷.社区对调查结果进行了整理,绘制了如下不完整的统计图表.被调查居民选择各选项人数统计表
雾霾天气的主要成因 | 频数(人数) |
A大气气压低,空气不流动 | m |
B地面灰尘大,空气湿度低 | 40 |
C汽车尾气排放 | n |
D工厂造成的污染 | 120 |
E其他 | 60 |
请根据图表中提供的信息解答下列问题:
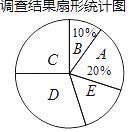
(1)填空:m=________,n=________,扇形统计图中C选项所占的百分比为________.
(2)若该社区居民约有6 000人,请估计其中会选择D选项的居民人数.
(3)对于“雾霾”这个环境问题,请你用简短的语言发出倡议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com