
����Ŀ�����������ҹ��ܶ����������������������ij����Ϊ�˵��鱾�������������������Ҫ�������ʶ���������Ը��������־���������ʾ����飬Ҫ�����������Ҫ������ֻѡ�����е�һ����������Ҫ����д���ʾ��������Ե��������������������������²�������ͳ��ͼ�������������ѡ���ѡ������ͳ�Ʊ�
������������Ҫ���� | Ƶ���������� |
A������ѹ�ͣ����������� | m |
B����ҳ�����ʪ�ȵ� | 40 |
C����β���ŷ� | n |
D������ɵ���Ⱦ | 120 |
E���� | 60 |
�����ͼ�����ṩ����Ϣ����������⣺
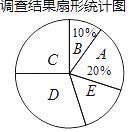
��1����գ�m=________��n=________������ͳ��ͼ��Cѡ����ռ�İٷֱ�Ϊ________��
��2��������������Լ��6 000�ˣ���������л�ѡ��Dѡ��ľ���������
��3������������������������⣬�����ü�̵����Է������飮
���𰸡���1��80��100��25%����2��1800�ˣ���3��������.
�������������������1������B��Ƶ��������ռ�ٷֱ���ñ��ε�������������ٸ���Ƶ��=������Ƶ�ʼ�����Ƶ��֮�͵�����������ɡ�
��2��������������������D�۵���ռ�ٷֱȼ��ɵá�
��3�����ݸ��ֹ۵���ռ�ٷֱȣ�����Ե���������ĸ���������ɡ�
�⣺��1���������⣬���ε����������Ϊ40��10%=400���ˣ���
��m=400��20%=80��n=400��(80+40+120+60)=100��
������ͳ��ͼ��Cѡ����ռ�İٷֱ�Ϊ![]() .
.
��2���⣺6000�� ![]() =1800���ˣ���
=1800���ˣ���
�𣺻�ѡ��Dѡ��ľ�������ԼΪ1800��
��3���⣺��������ȡ�����г�C��D���ֹ۵������ռ�������ı����ϴ�
���Գ�����Ļ����������ϸ���ƹ�������Ⱦ�ŷţ�ͬʱ����������������������˽�ҳ����еĴ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
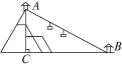
����Ŀ����1��ϲ����ɽ��ͬѧ��֪��,�ܶ���ɽ�϶��б������˹۹������,��ͼ��ʾ,ɽ�ĸ߶�ACΪ800 m,��ɽ��A��ɽ��B������һ������,��BC=1 500 m,һ�οʹ�ɽ�����������³���ɽ��,֪�³�ÿ������50 m,��ô��Լ�ʱ�����οͲ��ܵ���ɽ��?˵������.
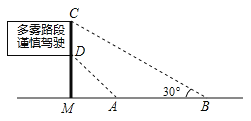
��2����ͼ���Ǵ����ڸ��ٹ�·ˮƽ�����ϵĽ�ͨ��ʾ�ƣ��������õ��������ݣ�AM=4�ף�AB=8�ף���MAD=45������MBC=30������ʾ�Ƶĸ߶�CD�������ȷ��0.1�ף��ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73����
��1.73����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲��±������ǰѱ�������ĸ�ĺ����õĶ���ʽ��Ϊ������������ʽ�������磺
��1��ġ�����������ʽ��Ϊ��![]() ��
��
��2��ġ�����������ʽ��Ϊ��![]() ��
��
�ش��������⣺
��1����3������������ʽ��Ϊ__________��4��ġ�����������ʽ��Ϊ____________
��![]() ��ġ�����������ʽ��Ϊ__________��
��ġ�����������ʽ��Ϊ__________��
��2������![]() �������������ʽ�������ʽ
�������������ʽ�������ʽ![]() �ĺͲ�����
�ĺͲ�����![]() ���ˡ�����������ʽ����
���ˡ�����������ʽ����
��� | 1 | 2 | 3 | 4 | ���� |
ͼ�� |
|
|
|
| ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
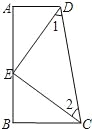
����Ŀ����ͼ��AD��BC����A=90����E��AB�ϵ�һ�㣬��AD=BE����1=��2��
��1��Rt��ADE��Rt��BECȫ������д����Ҫ���������̣�
��2����CED�Dz���ֱ�������Σ���˵�����ɣ�
��3������֪AD=6��AB=14��������������CED�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�BO��CO�ֱ�ƽ�֡�ABC����ACB������O��CEΪ��ǡ�ACD��ƽ���ߣ�BO���ӳ��߽�CE�ڵ�E���ǡ�BAC=��1����BEC=��2�������½��ۢ١�1=2��2���ڡ�BOC=3��2���ۡ�BOC=90��+��1���ܡ�BOC=90��+��2��ȷ���ǣ�������

A. �٢ڢ� B. �٢ۢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ������һ����װ���������װÿ����1200Ԫ�����ÿ������140Ԫ�������ڿ�չ������ڼ䣬����ͬʱ��ͻ��ṩ�����Żݷ�����
����һ����װ��һ�����
����װ������������۵�![]() �����ij�ͻ�Ҫ���÷�װ��������װ20�ף����
�����ij�ͻ�Ҫ���÷�װ��������װ20�ף����![]() ����
����![]() ����20��
����20��
��1�����ÿͻ��������ٹ����踶��_________Ԫ���ú�![]() ��ʽ�ӱ�ʾ�������ÿͻ��������ڹ����踶��_________Ԫ���ú�
��ʽ�ӱ�ʾ�������ÿͻ��������ڹ����踶��_________Ԫ���ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��2����![]() ��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
��3����![]() ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������֡�
��ͼ�����ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У���ABC������������ڸ���ϣ�

��1���밴Ҫ��ͼ������ABC�Ƶ�A��˳ʱ�뷽����ת90�㣬��B�Ķ�Ӧ��ΪB�䣬��C�Ķ�Ӧ��ΪC�䣬����BB�䣻
��2���ڣ�1������ͼ���У���AB��B=�� ����
����������
��ͼ�����ڵȱ�������ABC�У�AC=7����P����ABC�ڣ�����APC=90������BPC=120�㣬����APC�������
С��ͬѧͨ���۲졢������˼���������������γ��������뷨��
�뷨һ������APC�Ƶ�A��˳ʱ�뷽����ת60�㣬�õ���AP��B������PP�䣬Ѱ��PA��PB��PC�����߶�֮���������ϵ��
�뷨��������APB�Ƶ�A����ʱ�뷽����ת60�㣬�õ���AP��C�䣬����PP�䣬Ѱ��PA��PB��PC�����߶�֮���������ϵ��
��
��ο�С��ͬѧ���뷨����ɸ�����Ľ����̣���һ�ַ������ɣ�
��������á�
��ͼ�������ı���ABCD�У�AE��BC������ΪE����BAE=��ADC��BE=CE=2��CD=5��AD=kAB��kΪ����������BD�ij����ú�k��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=2������P�ӵ�B��������ÿ��1����λ���ٶ��������εı�����BC-CD-DA�˶������˶�ʱ��Ϊt,��PAB���ΪS.

(1)��S����t�ĺ�������ʽ����д���Ա���t��ȡֵ��Χ;
(2)������Ӧ����ͼ��;
(3)��S=![]() ʱ��t��ֵΪ����.
ʱ��t��ֵΪ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ:��֪DΪ����ֱ����ABCб��BC�ϵ�һ������(D��B��C�����غ�),����AD,��ADE�ǵ���ֱ��������,DEΪб��,����CE,���ECD�Ķ���.
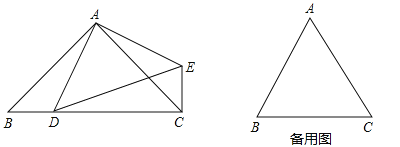
(2)��(1)����ABC����ADE����Ϊ�ȱ�������,D��Ϊ��ABC��BC���ϵ�һ������(D��B��C�����غ�),����D�˶���ʲôλ��ʱ,��DCE���ܳ���С?��̽���D��λ��,��˵������,�������ʱ��EDC�Ķ���.
(3)��(2)��������,����D�˶���ʹ��DCE���ܳ���Сʱ,��M�Ǵ�ʱ����AD�ϵ�һ������,��CMΪ��,��ֱ��CM���·����ȱ�������CMN,����ABC�ı߳�Ϊ4����ֱ��д��DN���ȵ���Сֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com