
【题目】如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )

A. ①②③ B. ①③④ C. ①④ D. ①②④
【答案】C
【解析】
根据三角形内角和定理以及三角形角平分线的定义可得∠BOC=90°+![]() ∠1,再结合三角形外角性质可得∠ECD=∠OBC+∠2,从而可得∠BOC=90°+∠2,据此即可进行判断.
∠1,再结合三角形外角性质可得∠ECD=∠OBC+∠2,从而可得∠BOC=90°+∠2,据此即可进行判断.
∵BO,CO分别平分∠ABC,∠ACB,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∵∠ABC+∠ACB+∠1=180°,
∴∠ABC+∠ACB=180°-∠1,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠1)=90°-
(180°-∠1)=90°-![]() ∠1,
∠1,
∴∠BOC=180°-∠OBC-∠OCB=180°-(90°-![]() ∠1)=90°+
∠1)=90°+![]() ∠1,
∠1,
∵∠ACD=∠ABC+∠1,CE平分∠ACD,
∴∠ECD=![]() ∠ACD=
∠ACD=![]() (∠ABC+∠1),
(∠ABC+∠1),
∵∠ECD=∠OBC+∠2,
∴∠2=![]() ∠1,即∠1=2∠2,
∠1,即∠1=2∠2,
∴∠BOC=90°+![]() ∠1=90°+∠2,
∠1=90°+∠2,
∴①④正确,②③错误,
故选C.


科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC,其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.

(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.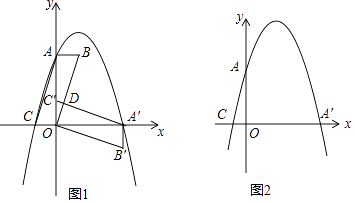
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( ) 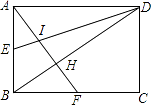
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴,y轴的正半轴上(OA<OB),且OA,OB的长分别是一元二次方程x2﹣14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,分别交x轴,y轴于点D,E.
(1)直接写出点A、B的坐标:A , B;
(2)求线段AD的长;
(3)已知P是直线CD上一个动点,点Q是直线AB上一个动点,则在坐标平面内是否存在点M,使得以点C、P、Q、M为顶点的四边形是以5为边长的正方形?若存在,直接写出点M的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com