
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪Rt��AOB����ֱ�DZ�OA��OB�ֱ���x�ᣬy����������ϣ�OA��OB������OA��OB�ij��ֱ���һԪ���η���x2��14x+48=0�����������߶�AB�Ĵ�ֱƽ����CD��AB�ڵ�C���ֱ�x�ᣬy���ڵ�D��E��
��1��ֱ��д����A��B�����꣺A �� B��
��2�����߶�AD�ij���
��3����֪P��ֱ��CD��һ�����㣬��Q��ֱ��AB��һ�����㣬��������ƽ�����Ƿ���ڵ�M��ʹ���Ե�C��P��Q��MΪ������ı�������5Ϊ�߳��������Σ������ڣ�ֱ��д����M�����ꣻ�������ڣ�˵�����ɣ�
���𰸡�
��1����6��0������0��8��
��2��
�⣺��Rt��AOB�У��ߡ�AOB=90�㣬OA=6��OB=8��
��AB= ![]() =10��
=10��
���߶�AB�Ĵ�ֱƽ����CD��AB�ڵ�C��
��AC= ![]() AB=5��
AB=5��
�ڡ�ACD���AOB�У�
�ߡ�CAD=��OAB����ACD=��AOB=90�㣬
���ACD�ס�AOB��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
���AD= ![]() ��
��
��A��6��0������D��x���ϣ�
��D���� ![]() ��0����
��0����
��ֱ��CD�Ľ���ʽΪy=kx+b��
������֪CΪAB�е㣬
��C��3��4����
��D���� ![]() ��0����
��0����
��  �����
����� ![]() ��
��
��ֱ��CD�Ľ���ʽΪy= ![]() x+
x+ ![]() ��
��
��3��
�⣺������ƽ���ڴ��ڵ�M��ʹ�Ե�C��P��Q��MΪ������ı����������Σ��Ҹ������εı߳�Ϊ5��
��AC=BC= ![]() AB=5��
AB=5��
���Ե�C��P��Q��MΪ����������εı߳�Ϊ5���ҵ�Q���B���A�غϣ������������
�� ����Q���B�غ�ʱ������BM�Ľ���ʽΪy= ![]() x+8����M��x��
x+8����M��x�� ![]() x+8����
x+8����
��B��0��8����BM=5��
�ࣨ ![]() x+8��8��2+x2=52��
x+8��8��2+x2=52��
������������x2=16��
���x=��4��
��M2��4��11����M3����4��5����
�ڵ���Q���A�غ�ʱ������AM�Ľ���ʽΪy= ![]() x��
x�� ![]() ��
��
��M��x�� ![]() x��
x�� ![]() ����
����
��A��6��0����AM=5��
�ࣨ ![]() x��
x�� ![]() ��2+��x��6��2=52��
��2+��x��6��2=52��
������������x2��12x+20=0��
���x1=2��x2=10��
��M4��2����3����M1��10��3����
���������������M������ΪM1��10��3����M2��4��11����M3����4��5����M4��2����3����
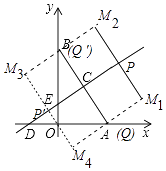
���������⣺��1���ⷽ��x2��14x+48=0��
��x1=6��x2=8��
��OA��OB��
��A��6��0����B��0��8����
���Դ��ǣ�6��0������0��8����
�����㾫�����������������ε��ж��ǽ����ĸ�������Ҫ֪�����������ε��ж�����:���Ƕ�Ӧ��ȣ������������ƣ�ASA����ֱ�������α�б���ϵĸ߷ֳɵ�����ֱ�������κ�ԭ���������ƣ� ���߶�Ӧ�ɱ����Ҽн���ȣ������������ƣ�SAS�������߶�Ӧ�ɱ����������������ƣ�SSS����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�BO��CO�ֱ�ƽ�֡�ABC����ACB������O��CEΪ��ǡ�ACD��ƽ���ߣ�BO���ӳ��߽�CE�ڵ�E���ǡ�BAC=��1����BEC=��2�������½��ۢ١�1=2��2���ڡ�BOC=3��2���ۡ�BOC=90��+��1���ܡ�BOC=90��+��2��ȷ���ǣ�������

A. �٢ڢ� B. �٢ۢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ĺ���Ϊ������֪��С����С��ѧϰ���ʳ���֪ʶ�������������Ϸ��С�������з���10��8��6�����˿��ƣ�С�������з���9��7��5�����˿��ƣ�ÿ�˴Ӹ�������ȡ��һ���ƽ��бȽϣ����ִ��Ϊ�����֡���ʤ��ÿ��ȡ���Ʋ��ܷŻأ�
��1����ÿ�����ȡ���е�һ���ƽ��б�������С�뱾���֡���ʤ�ĸ��ʣ�
��2������������������ʤ�ƣ���ʤ2�ֻ�3����Ϊ���α�����ʤ�ߣ���С���������Ƴ���˳��Ϊ�ȳ�6���ٳ�8������10ʱ��С���������Ӧ�ԣ���С�뱾�α�����ʤ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬��E��F�ֱ��ڱ�AB��BC�ϣ���ֱ��EF����EBF���ۣ�ʹ����B�Ķ�Ӧ��B1����AC���ϣ���EB1��AC����֤���ı���BFB1E�����Σ� 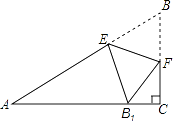
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2��2��k��1��x+k2=0��
��1����kΪ��ֵʱ��������ʵ������
��2����x1 �� x2�Ƿ��̵�����ʵ��������x12+x22=4����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����Ϊ18cm��ϸ��Χ��һ������������.
��1����������ǵױ߳���2�����������θ��ߵij���
��2����Χ����һ�ߵij���4cm�ĵ��������������ܣ�����������ߵij��������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ſ�Ϊ1cm�ľ���ֽ��������ţ������ص����ֲ������ı���ABCD�� 
��1�����ж��ı���ABCD����״����˵������
��2������BAD=30�㣬���ص����ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�k��1��x2����k��1��x+ ![]() =0��������ȵ�ʵ��������k��ֵ��
=0��������ȵ�ʵ��������k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬��A=30�㣬DE��ֱƽ��б��AC����AB��D��E�Ǵ��㣬����CD����BD=1����AC�ij��ǣ� �� 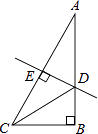
A.2 ![]()
B.2
C.4 ![]()
D.4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com