
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0,
(1)当k为何值时,方程有实数根;
(2)设x1 , x2是方程的两个实数根,且x12+x22=4,求k的值.
【答案】
(1)解:要使方程有实数根,必须△≥0
即4(k﹣1)2﹣4k2≥0
解得k≤ ![]() ,∴当k≤
,∴当k≤ ![]() 时,方程有实数根.
时,方程有实数根.
(2)解:由韦达定理得,x1+x2=2(k﹣1),x1x2=k2
∴x12+x22=(x1+x2)2﹣2x1x2
=4(k﹣1)2﹣2k2
=2k2﹣8k+4,
∵x12+x22=4,
∴2k2﹣8k+4=4
解得k1=0,k2=4,
由(1)知k≤ ![]() ,∴k=4不合题意,
,∴k=4不合题意,
∴k=0.
【解析】(1)根据△≥0,确定k的取值范围;(2)把x12+x22=4转化成(x1+x2)2﹣2x1x2=4,再把x1+x2=2(k﹣1),x1x2=k2代入,得到关于k的方程,即可求得k的值.
【考点精析】关于本题考查的求根公式和根与系数的关系,需要了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能得出正确答案.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】长城公司为希望小学捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.
(1)写出所有的选购方案(用列表法或树状图);
(2)如果在上述选购方案中,每种方案被选中的可能性相同,那么A型器材被选中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
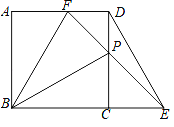
【题目】如图,在正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP=x,△PBF的面积为S1,△PDE的面积为S2
(1)求证:BP⊥DE;
(2)求S1﹣S2关于x的函数解析式,并写出x的取值范围;
(3)当∠PBF=30°时,求S1﹣S2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C时的视角∠BAC是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴,y轴的正半轴上(OA<OB),且OA,OB的长分别是一元二次方程x2﹣14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,分别交x轴,y轴于点D,E.
(1)直接写出点A、B的坐标:A , B;
(2)求线段AD的长;
(3)已知P是直线CD上一个动点,点Q是直线AB上一个动点,则在坐标平面内是否存在点M,使得以点C、P、Q、M为顶点的四边形是以5为边长的正方形?若存在,直接写出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你用学习“一次函数”时积累的经验和方法解决下列问题:
(1)在平面直角坐标系中,画出函数y=|x|的图象;
①列表填空:
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | … |
②描点、连线,在图所示的平面直角坐标系中画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|的两条不同类型的性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(﹣3,0)和B(1,0),与y轴交于点C,
(1)求抛物线的表达式;
(2)若点D为此抛物线上位于直线AC上方的一个动点,当△DAC的面积最大时,求点D的坐标;
(3)设抛物线顶点关于y轴的对称点为M,记抛物线在第二象限之间的部分为图象G.点N是抛物线对称轴上一动点,如果直线MN与图象G有公共点,请结合函数的图象,直接写出点N纵坐标t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com