
【题目】如图,在平行四边形ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DEBF是平行四边形.

【答案】解:∵四边形ABCD是平行四边形
∴AD∥BC,AB∥CD
∴∠CDB=∠ABD
∵DF平分∠CDB,BE平分∠ABD
∴∠FDB=1/2∠CDB, ∠EBD=1/2∠ABD
∴∠FDB=∠EBD
∴DF∥BE
∵AD∥BC,即ED∥BF
∴四边形DEBF是平行四边形
【解析】
根据四边形ABCD是平行四边形,由平行四边形的性质可得:AD∥BC,AB∥CD,
,∠CDB=∠ABD,根据DF平分∠CDB,BE平分∠ABD,利用角平分线的定义可得:∠FDB=![]() ∠CDB,∠EBD=
∠CDB,∠EBD=![]() ∠ABD,进而可得:∠FDB=∠EBD,根据平行线的判定可得:DF∥BE,
∠ABD,进而可得:∠FDB=∠EBD,根据平行线的判定可得:DF∥BE,
根据AD∥BC,即ED∥BF,利用平行四边形的判定可得:四边形DEBF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠CDB=∠ABD,
∵DF平分∠CDB,BE平分∠ABD,
∴∠FDB=![]() ∠CDB,∠EBD=
∠CDB,∠EBD=![]() ∠ABD,
∠ABD,
∴∠FDB=∠EBD,
∴DF∥BE,
∵AD∥BC,即ED∥BF,
∴四边形DEBF是平行四边形.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】为了参观上海世博会,某公司安排甲、乙两车分别从相距300千米的上海、泰州两地同时出发相向而行,甲到泰州带客后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图像. 
(1)请直接写出甲离出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量x的取值范围;
(2)当它们行驶4.5小时后离各自出发点的距离相等,求乙车离出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,甲、乙两车从各自出发地驶出后经过多少时间相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a≠0)(a≠0,a,b,C为常数)的图象,若关于x的一元二次方程ax2+bx+c=m有实数根,则m的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料
【材料一】按一定顺序排列的一列数称为数列,记作:{an}(n属于正整数).数列中的每一个数都叫做这个数列的项,排在第一位的数称为这个数列的第l项
(通常也叫做首项),记作:al;排在第二位的数称为这个数列的第2项,记作:a2;…;排在第打位的数称为这个数列的第n项,记作:an .
【材料二】如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列.这个常数叫做等差数列的公差,公差常用字母d表示.
例如:数列l0,l5,20,25是等差数列.
如果数列al , a2 , a3 , …,an , …是等差数列,那么a2﹣al=d,a3﹣a2=d,…,
an﹣an﹣l=d.即:a2=al+d,a3=a2+d=al+d+d=al+2d,a4=a3+d=al+3d,….
根据上述材料,解答问题
(1)下列数列属于等差数列的是 (只填序号).
①l,2,3,4,5.②2,4,6,8,10,11.③l,1,1,1,1.
(2)已知数列{an}是等差数列,
①al=1,a2=4,a3=7,….则al0= .
②首项a1=23,公差d=2,则an= .
(3)已知等差数列{an}满足a2=0,a6+a8=﹣10.求an .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )

A. ①②③ B. ①③④ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F. 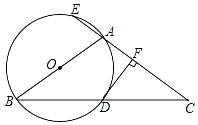
(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队准备开挖一条隧道,为了缩短工期,必须在山的两侧同时开挖,为了确保两侧开挖的隧道在同一条直线上,测量人员在如图所示的同一高度定出了两个开挖点P和Q,然后在左边定出开挖的方向线AP,为了准确定出右边开挖的方向线BQ,测量人员取一个可以同时看到点A,P,Q的点O,测得∠A=28°,∠AOC=100°,那么∠QBO应等于多少度才能确保BQ与AP在同一条直线上?
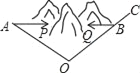
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0,
(1)当k为何值时,方程有实数根;
(2)设x1 , x2是方程的两个实数根,且x12+x22=4,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com