
【题目】某服装厂生产一种西装和领带,西装每套定价1200元,领带每条定价140元.厂方在开展促销活动期间,可以同时向客户提供两种优惠方案:
①买一套西装送一条领带
②西装和领带都按定价的![]() 付款,现某客户要到该服装厂购买西装20套,领带
付款,现某客户要到该服装厂购买西装20套,领带![]() 条(
条(![]() 超过20)
超过20)
(1)若该客户按方案①购买,需付款_________元(用含![]() 的式子表示);若该客户按方案②购买,需付款_________元(用含
的式子表示);若该客户按方案②购买,需付款_________元(用含![]() 的式子表示)
的式子表示)
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
(3)若![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
【答案】(1)(140x+21200);(126x+21600);(2)按方案②购买合算;(3)能,先按方案①购买20套西装,送20条领带,差18条领带按方案②购买,共需26268元.
【解析】
(1)方案①:计算20套西装的钱数再加上(x-20)条领带的钱数即可,方案②:计算20套西装和20条领带的钱数之和再乘以90%即可;
(2)将x=38分别代入代入两种方案所列的代数式,计算出结果再比较大小即可.
(3)根据两种方案的优惠方式,可得出先按方案①购买20套西装,送20条领带,差18条领带再按方案②购买即可.
(1)方案①: 1200×20+140(x-20)=(140x+21200)元,
方案②:(1200×20+140x)×90%=(126x+21600)元;
故答案为:(140x+21200);(126x+21600);
(2)当x=38时,方案①需140x+21200=140×38+21200=26520元,
方案②需126x+21600=126×38+21600=26388元,
∵26388元<26520元元,∴按方案②购买合算;
(3)能,先按方案①购买20套西装,送20条领带,差18条领带按方案②购买,
∴共需1200×20+140×18×90%=26268元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
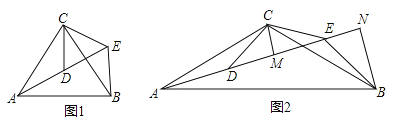
【题目】(2016山东省菏泽市)如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=![]() CM+
CM+![]() BN.
BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
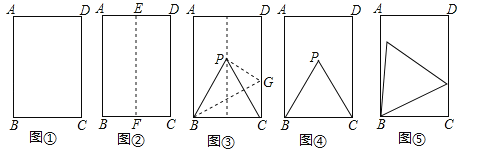
【题目】折纸的思考.
(操作体验)
用一张矩形纸片折等边三角形.
第一步,对折矩形纸片ABCD(AB>BC)(图①),使AB与DC重合,得到折痕EF,把纸片展平(图②).
第二步,如图③,再一次折叠纸片,使点C落在EF上的P处,并使折痕经过点B,得到折痕BG,折出PB,PC,得到△PBC.
(1)说明△PBC是等边三角形.
(数学思考)
(2)如图④,小明画出了图③的矩形ABCD和等边三角形PBC,他发现,在矩形ABCD中把△PBC经过图形变化,可以得到图⑤中的更大的等边三角形,请描述图形变化的过程.
(3)已知矩形一边长为3cm,另一边长为a cm,对于每一个确定的a的值,在矩形中都能画出最大的等边三角形,请画出不同情形的示意图,并写出对应的a的取值范围.
(问题解决)
(4)用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片,所需正方形铁片的边长的最小值为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…则点A2017的坐标是( )
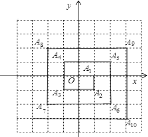
A.(505,504)B.(﹣503,﹣504 )C.(503,﹣503)D.(﹣504,504)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国很多地区持续出现雾霾天气.某社区为了调查本社区居民对雾霾天气主要成因的认识情况,随机对该社区部分居民进行了问卷调查,要求居民从五个主要成因中只选择其中的一项,被调查居民都按要求填写了问卷.社区对调查结果进行了整理,绘制了如下不完整的统计图表.被调查居民选择各选项人数统计表
雾霾天气的主要成因 | 频数(人数) |
A大气气压低,空气不流动 | m |
B地面灰尘大,空气湿度低 | 40 |
C汽车尾气排放 | n |
D工厂造成的污染 | 120 |
E其他 | 60 |
请根据图表中提供的信息解答下列问题:
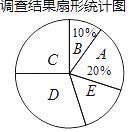
(1)填空:m=________,n=________,扇形统计图中C选项所占的百分比为________.
(2)若该社区居民约有6 000人,请估计其中会选择D选项的居民人数.
(3)对于“雾霾”这个环境问题,请你用简短的语言发出倡议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】岳麓山是旅游胜地,据统计2019年9月30日岳麓山旅游人数为2万人,十一黄金周期间,岳麓山7天中每天旅游人数的变化情况如下表(正数表示比9月30日多的人数,负数表示比9月30日少的人数):

(1)请判断7天内游客人数量最多和最少的各是哪一天?它们相差多少万人?
(2)求这7天去岳麓山旅游的总人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数轴上的A、B、C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“至善点”.例如:若数轴上点A、B、C所表示的数分别为1、3、4,则点B是点A、C的“至善点”.
(1)若点A表示数﹣2,点B表示数2,下列各数![]() 、0、1、6所对应的点分别为C1、C2、C3、C4,其中是点A、B的“至善点”的有 (填代号);
、0、1、6所对应的点分别为C1、C2、C3、C4,其中是点A、B的“至善点”的有 (填代号);
(2)已知点A表示数﹣1,点B表示数3,点M为数轴上一个动点:
①若点M在点A的左侧,且点M是点A、B的“至善点”,求此时点M表示的数m;
②若点M在点B的右侧,点M、A、B中,有一个点恰好是其它两个点的“至善点”,求出此时点M表示的数m.
查看答案和解析>>
科目:初中数学 来源: 题型:
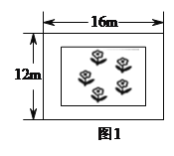
【题目】在一块长![]() ,宽为
,宽为![]() 的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
(![]() )小芳说,‘我的设计方案如图所示,平行于荒地的四边建造矩形的花园,花园四周小路的宽度均相同’,你能帮小芳算出小路的宽度吗?请利用方程的方法计算出小路的宽度.
)小芳说,‘我的设计方案如图所示,平行于荒地的四边建造矩形的花园,花园四周小路的宽度均相同’,你能帮小芳算出小路的宽度吗?请利用方程的方法计算出小路的宽度.
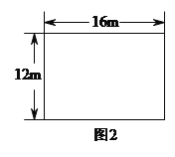
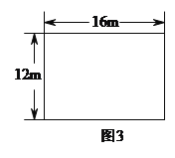
(![]() )小华说,‘我的设计方案是建造一个中心对称的四边形的花园,并且这个四边形的四个顶点分别在矩形荒地的四条边上’,请你按小华的思路,分别设计符合条件的一个菱形和一个矩形,在图
)小华说,‘我的设计方案是建造一个中心对称的四边形的花园,并且这个四边形的四个顶点分别在矩形荒地的四条边上’,请你按小华的思路,分别设计符合条件的一个菱形和一个矩形,在图![]() 和图
和图![]() 中画出相应的草图,说明所画图形的特征,并简述所画图形符合要求的理由.
中画出相应的草图,说明所画图形的特征,并简述所画图形符合要求的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
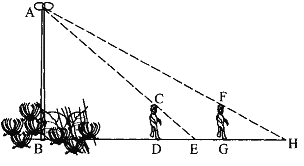
【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com