
����Ŀ����ֽ��˼����
���������飩
��һ�ž���ֽƬ�۵ȱ������Σ�
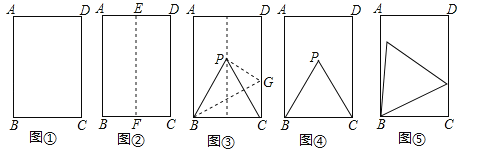
��һ�������۾���ֽƬABCD��AB��BC����ͼ�٣���ʹAB��DC�غϣ��õ��ۺ�EF����ֽƬչƽ��ͼ������
�ڶ�������ͼ�ۣ���һ���۵�ֽƬ��ʹ��C����EF�ϵ�P������ʹ�ۺ۾�����B���õ��ۺ�BG���۳�PB��PC���õ���PBC��
��1��˵����PBC�ǵȱ������Σ�
����ѧ˼����
��2����ͼ�ܣ�С��������ͼ�۵ľ���ABCD�͵ȱ�������PBC�������֣��ھ���ABCD�а���PBC����ͼ�α仯�����Եõ�ͼ���еĸ���ĵȱ������Σ�������ͼ�α仯�Ĺ��̣�
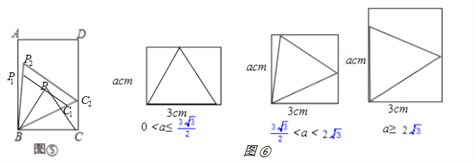
��3����֪����һ�߳�Ϊ3cm����һ�߳�Ϊa cm������ÿһ��ȷ����a��ֵ���ھ����ж��ܻ������ĵȱ������Σ��뻭����ͬ���ε�ʾ��ͼ����д����Ӧ��a��ȡֵ��Χ��
����������
��4����һ����������Ƭ��һ��ֱ�DZ߳��ֱ�Ϊ4cm��1cm��ֱ����������Ƭ��������������Ƭ�ı߳�����СֵΪ cm��
���𰸡���1�����ɼ���������2���𰸼���������3������𰸲�Ψһ����ͼ�ޣ���4��![]() ��
��
�����������⣨1�����۵������ʺʹ�ֱƽ���ߵ����ʵó�PB=PC��PB=CB���ó�PB=PC=CB���ɣ�
��2������ת�����ʺ�λ�Ƶ����ʼ��ɵó��𰸣�
��3���ɵȱ������ε����ʡ�ֱ�������ε����ʡ����ɶ������м��㣬����ͼ�μ��ɣ�
��4��֤����AEF����DCE���ó�![]() ����AE=x����AD=CD=4x��DE=AD��AE=3x����Rt��CDE�У��ɹ��ɶ����ó����̣��ⷽ�̼��ɣ�
����AE=x����AD=CD=4x��DE=AD��AE=3x����Rt��CDE�У��ɹ��ɶ����ó����̣��ⷽ�̼��ɣ�
����������⣺��1�����۵������ʵã�EF��BC�Ĵ�ֱƽ���ߣ�BG��PC�Ĵ�ֱƽ���ߣ���PB=PC��PB=CB����PB=PC=CB������PBC�ǵȱ������Σ�
��2����![]() ��BΪ���ģ��ھ���ABCD�а���PBC��ʱ�뷽����ת�ʵ��ĽǶȣ��õ���P1BC1��
��BΪ���ģ��ھ���ABCD�а���PBC��ʱ�뷽����ת�ʵ��ĽǶȣ��õ���P1BC1��
���Ե�BΪλ�����ģ�������P1BC1�Ŵ�ʹ��C1�Ķ�Ӧ��C2����CD�ϣ��õ���P2BC2��
��ͼ����ʾ��
��3������𰸲�Ψһ��������ͼ����ʾ��
��4����ͼ����ʾ��
��CEF��ֱ�������Σ���CEF=90�㣬CE=4��EF=1�����AEF+��CED=90�㣬���ı���ABCD�������Σ����A=��D=90�㣬AD=CD�����DCE+��CED=90�㣬���AEF=��DCE������AEF����DCE����![]() ����AE=x����AD=CD=4x����DE=AD��AE=3x����Rt��CDE�У��ɹ��ɶ����ã�
����AE=x����AD=CD=4x����DE=AD��AE=3x����Rt��CDE�У��ɹ��ɶ����ã�![]() ����ã�x=
����ã�x=![]() ����AD=4��
����AD=4��![]() =
=![]() ���ʴ�Ϊ��
���ʴ�Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�ˡ��������꼶����ѧ��180�ˣ�Ϊ�˽��������꼶ѧ�������ʽ�������������˳������飬�������£��벹��������
�ռ�����
�Ӱˡ��������꼶�������ȡ![]() ��ѧ�������������ʽ������ԣ����Գɼ����ٷ��ƣ����£�
��ѧ�������������ʽ������ԣ����Գɼ����ٷ��ƣ����£�
���꼶 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
���꼶 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
��������������
�����·����������������������������ݣ�
|
|
|
|
|
| |
���꼶 | 0 | 0 | 1 | 11 | 1 | |
���꼶 | 1 | 0 | 0 | 7 |
��˵�����ɼ�![]() �ּ�����Ϊ���ʽ������㣬
�ּ�����Ϊ���ʽ������㣬![]() ~
~![]() ��Ϊ���ʽ������ã�
��Ϊ���ʽ������ã�![]() ~
~![]() ��Ϊ���ʽ����ϸ�
��Ϊ���ʽ����ϸ�![]() ������Ϊ���ʽ������ϸ�
������Ϊ���ʽ������ϸ�
��������
�����������ݵ�ƽ��������λ�����������������±���ʾ��
�꼶 | ƽ���� | ��λ�� | ���� | ���� |
���꼶 |
|
|
| 33.6 |
���꼶 |
|
| 52.1 |
�뽫������������������
����
��1�����ƾ��꼶���ʽ��������ѧ������Ϊ__________��
��2�������ƶϳ�_______�꼶ѧ�������ʽ����������һЩ������Ϊ_________________�������ٴ�������ͬ�ĽǶ�˵���ƶϵĺ����ԣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
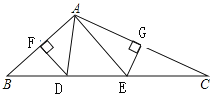
����Ŀ����ͼ,��ABC��,AB,AC�ߵĴ�ֱƽ���߷ֱ�BC�ڵ�D,E,����ֱ�Ϊ��F,G,��ADE���ܳ�Ϊ6cm
(1)����ABC��BC�ߵij���;(2)����B+��C=64��,���DAE�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ3��С����5��д�Ų�ͬ���ֵĿ�Ƭ�����㰴Ҫ������Ƭ������������⣮
��1�����г�ȡ2�ſ�Ƭ��ʹ��2�ſ�Ƭ�����ֵij˻�������ֵ�Ƕ��٣�д�����ֵ������ʽ��
��2�����г�ȡ2�ſ�Ƭ��ʹ��2�ſ�Ƭ���������������С����Сֵ�Ƕ��٣�д����Сֵ������ʽ��
��3�����г�ȡ��0�����4�ſ�Ƭ������4�����ֽ��мӡ������ˡ������˷�������㣬ÿ������ֻ����һ�Σ�ʹ���Ϊ24��д����������ʽ�ӣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲��±������ǰѱ�������ĸ�ĺ����õĶ���ʽ��Ϊ������������ʽ�������磺
��1��ġ�����������ʽ��Ϊ��![]() ��
��
��2��ġ�����������ʽ��Ϊ��![]() ��
��
�ش��������⣺
��1����3������������ʽ��Ϊ__________��4��ġ�����������ʽ��Ϊ____________
��![]() ��ġ�����������ʽ��Ϊ__________��
��ġ�����������ʽ��Ϊ__________��
��2������![]() �������������ʽ�������ʽ
�������������ʽ�������ʽ![]() �ĺͲ�����
�ĺͲ�����![]() ���ˡ�����������ʽ����
���ˡ�����������ʽ����
��� | 1 | 2 | 3 | 4 | ���� |
ͼ�� |
|
|
|
| ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������4��ȫ�ȵ�С��������1��С���������̶��ɵ�������ͼ��.��֪��ͼ�������Ϊ49��С�����ε����Ϊ4�����ֱ���x��y(x >y)��ʾС�����εij��Ϳ��������й�ϵʽ�в���ȷ����( )

A. x+y=7 B. x-y=2 C. x2 +y2=25 D. 4xy+4=49
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
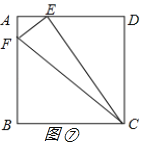
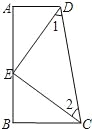
����Ŀ����ͼ��AD��BC����A=90����E��AB�ϵ�һ�㣬��AD=BE����1=��2��
��1��Rt��ADE��Rt��BECȫ������д����Ҫ���������̣�
��2����CED�Dz���ֱ�������Σ���˵�����ɣ�
��3������֪AD=6��AB=14��������������CED�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ������һ����װ���������װÿ����1200Ԫ�����ÿ������140Ԫ�������ڿ�չ������ڼ䣬����ͬʱ��ͻ��ṩ�����Żݷ�����
����һ����װ��һ�����
����װ������������۵�![]() �����ij�ͻ�Ҫ���÷�װ��������װ20�ף����
�����ij�ͻ�Ҫ���÷�װ��������װ20�ף����![]() ����
����![]() ����20��
����20��
��1�����ÿͻ��������ٹ����踶��_________Ԫ���ú�![]() ��ʽ�ӱ�ʾ�������ÿͻ��������ڹ����踶��_________Ԫ���ú�
��ʽ�ӱ�ʾ�������ÿͻ��������ڹ����踶��_________Ԫ���ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��2����![]() ��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
��3����![]() ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ���ѧ�һ�����һ�γ�������;�У������ɻ��������ij˿��Ķ�����־����һ�������⣬��![]() ��������.�����ѿڶ���,��֪������Ѹ��ȷ�ؼ������������밴�������������һ�ԣ�
��������.�����ѿڶ���,��֪������Ѹ��ȷ�ؼ������������밴�������������һ�ԣ�
��1����![]() ,ȷ��
,ȷ��![]() ���������� λ����
���������� ���
��2����![]() �ĸ�λ����
�ĸ�λ����![]() ȷ��
ȷ��![]() ���������ĸ�λ���� ��
���������ĸ�λ���� ��
��3�������ȥ![]() �������λ
�������λ![]() �õ���
�õ���![]() ,��
,��![]() ,�ɴ���ȷ��
,�ɴ���ȷ��![]() ����������ʮλ���� ������
����������ʮλ���� ������![]() ���������� ��
���������� ��
��4�������Ƶķ�������˵��![]() ���������� .
���������� .
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com