
【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从八、九两个年级各随机抽取![]() 名学生,进行了体质健康测试,测试成绩(百分制)如下:
名学生,进行了体质健康测试,测试成绩(百分制)如下:
八年级 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
九年级 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按如下分数段整理、描述这两组样本数据:
|
|
|
|
|
| |
八年级 | 0 | 0 | 1 | 11 | 1 | |
九年级 | 1 | 0 | 0 | 7 |
(说明:成绩![]() 分及以上为体质健康优秀,
分及以上为体质健康优秀,![]() ~
~![]() 分为体质健康良好,
分为体质健康良好,![]() ~
~![]() 分为体质健康合格,
分为体质健康合格,![]() 分以下为体质健康不合格)
分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如下表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 |
|
|
| 33.6 |
九年级 |
|
| 52.1 |
请将以上两个表格补充完整;
得出结论
(1)估计九年级体质健康优秀的学生人数为__________;
(2)可以推断出_______年级学生的体质健康情况更好一些,理由为_________________.(至少从两个不同的角度说明推断的合理性).
科目:初中数学 来源: 题型:
【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,解答后面的问题:“十字相乘法”能将二次三项式分解因式,对于形如![]() 的关于
的关于![]() ,
,![]() 的二次三项式来说,方法的关键是将
的二次三项式来说,方法的关键是将![]() 项系数
项系数![]() 分解成两个因数
分解成两个因数![]() ,
,![]() 的积,即
的积,即![]() ,将
,将![]() 项系数
项系数![]() 分解成两个因式
分解成两个因式![]() ,
,![]() 的积,即
的积,即![]() ,并使
,并使![]() 正好等于
正好等于![]() 项的系数
项的系数![]() ,那么可以直接写成结果:
,那么可以直接写成结果:![]()
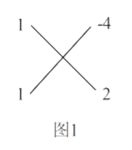
例:分解因式:![]()
解:如图1,其中![]() ,
,![]() ,而
,而![]()
所以![]()
而对于形如![]() 的关于
的关于![]() ,
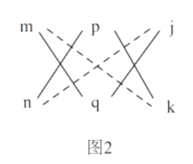
,![]() 的二元二次式也可以用十字相乘法来分解.如图2.将
的二元二次式也可以用十字相乘法来分解.如图2.将![]() 分解成
分解成![]() 乘积作为一列,
乘积作为一列,![]() 分解成
分解成![]() 乘积作为第二列,
乘积作为第二列,![]() 分解成
分解成![]() 乘积作为第三列,如果
乘积作为第三列,如果![]() ,
,![]() ,即第1、2列,第2、3列和第1、3列都满足十字相乘规则,则原式
,即第1、2列,第2、3列和第1、3列都满足十字相乘规则,则原式![]()
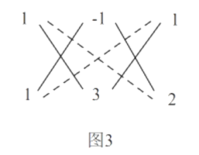
例:分解因式![]()
解:如图3,其中![]() ,
,![]() ,
,![]()
而![]() ,
,![]() ,
,![]()
所以![]()
请同学们通过阅读上述材料,完成下列问题:
(1)分解因式:①![]() .
.
②![]() .
.
(2)若关于![]() ,
,![]() 的二元二次式
的二元二次式![]() 可以分解成两个一次因式的积,求
可以分解成两个一次因式的积,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,下列叙述正确的是( )

A. 甲乙两地相距1200千米
B. 快车的速度是80千米∕小时
C. 慢车的速度是60千米∕小时
D. 快车到达甲地时,慢车距离乙地100千米
查看答案和解析>>
科目:初中数学 来源: 题型:
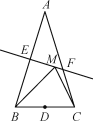
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
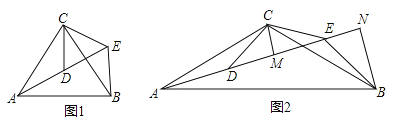
【题目】(2016山东省菏泽市)如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=![]() CM+
CM+![]() BN.
BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折纸的思考.
(操作体验)
用一张矩形纸片折等边三角形.
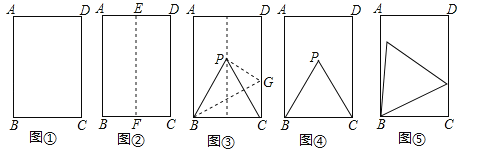
第一步,对折矩形纸片ABCD(AB>BC)(图①),使AB与DC重合,得到折痕EF,把纸片展平(图②).
第二步,如图③,再一次折叠纸片,使点C落在EF上的P处,并使折痕经过点B,得到折痕BG,折出PB,PC,得到△PBC.
(1)说明△PBC是等边三角形.
(数学思考)
(2)如图④,小明画出了图③的矩形ABCD和等边三角形PBC,他发现,在矩形ABCD中把△PBC经过图形变化,可以得到图⑤中的更大的等边三角形,请描述图形变化的过程.
(3)已知矩形一边长为3cm,另一边长为a cm,对于每一个确定的a的值,在矩形中都能画出最大的等边三角形,请画出不同情形的示意图,并写出对应的a的取值范围.
(问题解决)
(4)用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片,所需正方形铁片的边长的最小值为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com