
【题目】我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题,求![]() 的立方根.华罗庚脱口而出,你知道怎样迅速准确地计算出结果的吗?请按照下面的问题试一试:
的立方根.华罗庚脱口而出,你知道怎样迅速准确地计算出结果的吗?请按照下面的问题试一试:
(1)由![]() ,确定
,确定![]() 的立方根是 位数;
的立方根是 位数;
(2)由![]() 的个位数是
的个位数是![]() 确定
确定![]() 的立方根的个位数是 ;
的立方根的个位数是 ;
(3)如果划去![]() 后面的三位
后面的三位![]() 得到数
得到数![]() ,而
,而![]() ,由此能确定
,由此能确定![]() 的立方根的十位数是 ;所以
的立方根的十位数是 ;所以![]() 的立方根是 ;
的立方根是 ;
(4)用类似的方法,请说出![]() 的立方根是 .
的立方根是 .
【答案】(1)两;(2)9;(3)3,39;(4)![]()
【解析】
(1)根据59319大于1000而小于1000000,即可确定59319的立方根是两位数;
(2)根据一个数的立方的个位数就是这个数的个位数的立方的个位数,据此即可确定;
(3)根据数的立方的计算方法即可确定;
(4)首先根据一个数的立方的个位数就是这个数的个位数的立方的个位数确定个位数,然后一次确定十位数,即可求得立方根;
解:(1)∵1000<59319<1000000,
∴![]() ,
,
∴![]() 的立方根是两位数,
的立方根是两位数,
故答案为:两;
(2)只有个位数是9的立方数的个位数依然是9,
∴![]() 的立方根的个位数是9,
的立方根的个位数是9,
故答案为:9;
(3)∵27<59<64,
∴![]() ,
,
∴![]() 的十位数是3,
的十位数是3,
∴![]() ,
,
故答案为:3,39;
(4)根据上述知识可知,
∴![]() 是个负两位数,十位上的数是4,个位上的数是8,则
是个负两位数,十位上的数是4,个位上的数是8,则
![]() ,
,
故答案为:![]() ;
;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】折纸的思考.
(操作体验)
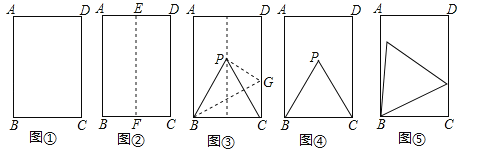
用一张矩形纸片折等边三角形.
第一步,对折矩形纸片ABCD(AB>BC)(图①),使AB与DC重合,得到折痕EF,把纸片展平(图②).
第二步,如图③,再一次折叠纸片,使点C落在EF上的P处,并使折痕经过点B,得到折痕BG,折出PB,PC,得到△PBC.
(1)说明△PBC是等边三角形.
(数学思考)
(2)如图④,小明画出了图③的矩形ABCD和等边三角形PBC,他发现,在矩形ABCD中把△PBC经过图形变化,可以得到图⑤中的更大的等边三角形,请描述图形变化的过程.
(3)已知矩形一边长为3cm,另一边长为a cm,对于每一个确定的a的值,在矩形中都能画出最大的等边三角形,请画出不同情形的示意图,并写出对应的a的取值范围.
(问题解决)
(4)用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片,所需正方形铁片的边长的最小值为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数轴上的A、B、C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“至善点”.例如:若数轴上点A、B、C所表示的数分别为1、3、4,则点B是点A、C的“至善点”.
(1)若点A表示数﹣2,点B表示数2,下列各数![]() 、0、1、6所对应的点分别为C1、C2、C3、C4,其中是点A、B的“至善点”的有 (填代号);
、0、1、6所对应的点分别为C1、C2、C3、C4,其中是点A、B的“至善点”的有 (填代号);
(2)已知点A表示数﹣1,点B表示数3,点M为数轴上一个动点:
①若点M在点A的左侧,且点M是点A、B的“至善点”,求此时点M表示的数m;
②若点M在点B的右侧,点M、A、B中,有一个点恰好是其它两个点的“至善点”,求出此时点M表示的数m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块长![]() ,宽为
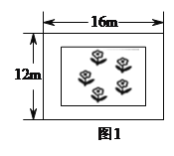
,宽为![]() 的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
(![]() )小芳说,‘我的设计方案如图所示,平行于荒地的四边建造矩形的花园,花园四周小路的宽度均相同’,你能帮小芳算出小路的宽度吗?请利用方程的方法计算出小路的宽度.
)小芳说,‘我的设计方案如图所示,平行于荒地的四边建造矩形的花园,花园四周小路的宽度均相同’,你能帮小芳算出小路的宽度吗?请利用方程的方法计算出小路的宽度.
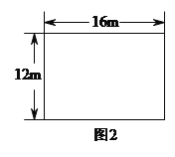
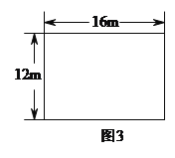
(![]() )小华说,‘我的设计方案是建造一个中心对称的四边形的花园,并且这个四边形的四个顶点分别在矩形荒地的四条边上’,请你按小华的思路,分别设计符合条件的一个菱形和一个矩形,在图
)小华说,‘我的设计方案是建造一个中心对称的四边形的花园,并且这个四边形的四个顶点分别在矩形荒地的四条边上’,请你按小华的思路,分别设计符合条件的一个菱形和一个矩形,在图![]() 和图
和图![]() 中画出相应的草图,说明所画图形的特征,并简述所画图形符合要求的理由.
中画出相应的草图,说明所画图形的特征,并简述所画图形符合要求的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E.
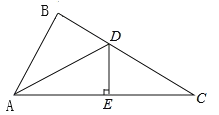
(1)证明∠BAD=∠C;
(2)∠BAD=29°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
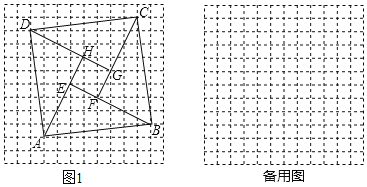
【题目】在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形ABCD的边为斜边,向内作四个全等的直角三角形,使四个直角顶点E,F,G,H都是格点,且四边形EFGH为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形ABCD的边长为![]() ,此时正方形EFGH的而积为5.问:当格点弦图中的正方形ABCD的边长为
,此时正方形EFGH的而积为5.问:当格点弦图中的正方形ABCD的边长为![]() 时,正方形EFGH的面积的所有可能值是_____(不包括5).
时,正方形EFGH的面积的所有可能值是_____(不包括5).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正两位数的个位数字是a,十位数字比个位数字大2.
(1)列式表示这个两位数;
(2)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新数与原数的和能被22整除.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
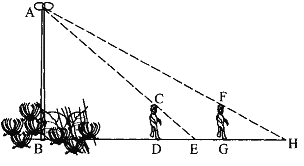
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com