练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

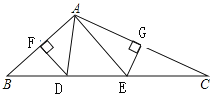
    【题目】如图,△ABC中,AB,AC边的垂直平分线分别交BC于点D,E,垂足分别为点F,G,△ADE的周长为6cm

    (1)求△ABC中BC边的长度;(2)若∠B+∠C=64°,求∠DAE的度数.

    【答案】（1）6;(2)52°.

    【解析】

    （1）根据垂直平分线的性质即可得到BD=AD,AE=CE，再根据周长的定义即可求解；

    （2）根据等腰三角形的性质及三角形的内角和即可求解.

    解：（1）∵DF垂直平分AB，EG垂线平分AC

    ∴AD=DB,AE=EC

    ∵△ADE的周长=AD+DE+AE=6

    ∴BC=BD+DE+EC=AD+DE+AE=6

    ∴BC=6

    (2) ∵AD=DB,AE=EC

    ∴∠BAD=∠B,∠EAC=∠C.

    ∵∠B+∠C=64°

    ∴∠BAD+∠EAC=64°

    ∴∠DAE=180°-（∠B+∠C+∠BAD+∠EAC）=52°

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料，解答后面的问题：“十字相乘法”能将二次三项式分解因式，对于形如的关于，的二次三项式来说，方法的关键是将项系数分解成两个因数，的积，即，将项系数分解成两个因式，的积，即，并使正好等于项的系数，那么可以直接写成结果：

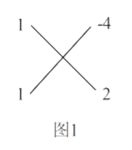
    例：分解因式：

    解：如图1，其中，，而

    所以

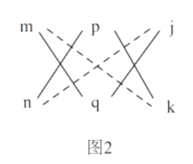
    而对于形如的关于，的二元二次式也可以用十字相乘法来分解．如图2．将分解成乘积作为一列，分解成乘积作为第二列，分解成乘积作为第三列，如果，，即第1、2列，第2、3列和第1、3列都满足十字相乘规则，则原式

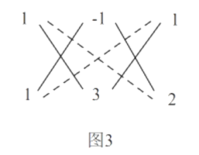
    例：分解因式

    解：如图3，其中，，

    而，，

    所以

    请同学们通过阅读上述材料，完成下列问题：

    （1）分解因式：① ．

    ② ．

    （2）若关于，的二元二次式可以分解成两个一次因式的积，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，AD⊥BC于D点，E、F分别为DB、DC的中点，则图中共有全等三角形 对．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

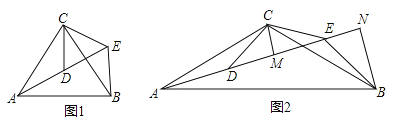
    【题目】（2016山东省菏泽市）如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．

    （1）如图1，若∠CAB=∠CBA=∠CDE=∠CED=50°

    ①求证：AD=BE；

    ②求∠AEB的度数．

    （2）如图2，若∠ACB=∠DCE=120°，CM为△DCE中DE边上的高，BN为△ABE中AE边上的高，试证明：AE=CM+BN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点，在数轴上分别表示有理数，．

    （1）对照数轴填写下表：

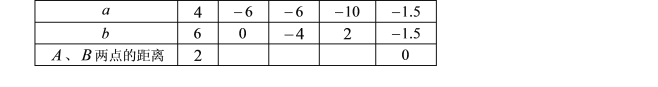
    （2）若，两点间的距离记为，试问和，有何数量关系；

    （3）写出数轴上到和的距离之和为的所有整数；

    （4）若表示一个有理数，求的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在平面直角坐标系中有 A(-2，1)， B(3， 1)，C(2， 3)三点，请回答下列问题:

    (1)在坐标系内描出点A， B， C的位置.

    (2)画出关于直线x=-1对称的，并写出各点坐标.

    (3)在y轴上是否存在点P，使以A，B， P三点为顶点的三角形的面积为10?若存在，请直接写出点P的坐标:若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

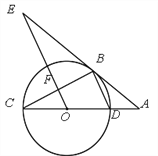
    【题目】如图，CD为⊙O的直径，点B在⊙O上，连接BC、BD，过点B的切线AE与CD的延长线交于点A， ，OE交BC于点F.

    （1）求证：OE∥BD；

    （2）当⊙O的半径为5， 时，求EF的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】折纸的思考．

    （操作体验）

    用一张矩形纸片折等边三角形．

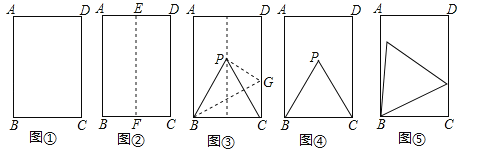
    第一步，对折矩形纸片ABCD（AB＞BC）（图①），使AB与DC重合，得到折痕EF，把纸片展平（图②）．

    第二步，如图③，再一次折叠纸片，使点C落在EF上的P处，并使折痕经过点B，得到折痕BG，折出PB，PC，得到△PBC．

    （1）说明△PBC是等边三角形．

    （数学思考）

    （2）如图④，小明画出了图③的矩形ABCD和等边三角形PBC，他发现，在矩形ABCD中把△PBC经过图形变化，可以得到图⑤中的更大的等边三角形，请描述图形变化的过程．

    （3）已知矩形一边长为3cm，另一边长为a cm，对于每一个确定的a的值，在矩形中都能画出最大的等边三角形，请画出不同情形的示意图，并写出对应的a的取值范围．

    （问题解决）

    （4）用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片，所需正方形铁片的边长的最小值为 cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于数轴上的A、B、C三点，给出如下定义：若其中一个点与其它两个点的距离恰好满足2倍的数量关系，则称该点是其它两个点的“至善点”．例如：若数轴上点A、B、C所表示的数分别为1、3、4，则点B是点A、C的“至善点”．

    （1）若点A表示数﹣2，点B表示数2，下列各数、0、1、6所对应的点分别为C1、C2、C3、C4，其中是点A、B的“至善点”的有　 　（填代号）；

    （2）已知点A表示数﹣1，点B表示数3，点M为数轴上一个动点：

    ①若点M在点A的左侧，且点M是点A、B的“至善点”，求此时点M表示的数m；

    ②若点M在点B的右侧，点M、A、B中，有一个点恰好是其它两个点的“至善点”，求出此时点M表示的数m．

    查看答案和解析>>

    同步练习册答案