【题目】如图,在公路 MN 两侧分别有 A
, A
......A
,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是（ ）.
①车站的位置设在 C 点好于 B 点;
②车站的位置设在 B 点与 C 点之问公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关.
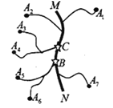
A.①B.②C.①③D.②③
【答案】C
【解析】
设出7条小公路的长度，然后分别表示出以B、C为车站时的距离之和，最后进行比较即可.
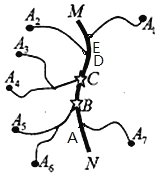
如图，设A1，A2，…，A7，七个工厂与公路MN连接的小公路的长度分别为a1，a2，…，a7，DE=u1，CD=u2，BC=u3，AB=u4，则
当以C为车站时：
距离和= a1+u1+u2+a2+u2+a3+a4+a5+u3+a6+u3+a7+u3+u4
= a1+a2+a3+a4+a5+a6+a7+u1+2u2+3u3+u4，
当以B为车站时：
距离和= a1+u1+u2+u3+a2+u2+u3+a3+u3+a4+u3+a5+a6+a7+u4
= a1+a2+a3+a4+a5+a6+a7+u1+2u2 +4u3 +u4
通过比较可知，车站的位置设在C点好于B点，且与各段小公路的长度无关.
故选：C.
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案科目：初中数学 来源： 题型：
【题目】如图，下列条件不能推出△ABC是等腰三角形的是（ ）
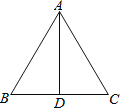
A. ∠B＝∠CB. AD⊥BC，∠BAD＝∠CAD
C. AD⊥BC，BD＝CDD. AD⊥BC，∠BAD＝∠ACD
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义一种对正整数n的“F”运算：①当n为奇数时，F（n）=3n+1；②当n为偶数时，F（n）=
（其中k是使F（n）为奇数的正整数）……，两种运算交替重复进行，例如，取n=24，则：
若n=13，则第2018次“F”运算的结果是（ ）
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某花农培育甲种花木10株，乙种花木8株，共需成本6400元；培育甲种花木4株，乙种花木5株，共需成本3100元。
（1）求甲乙两种花木成本分别是多少元？
（2）若1株甲种花木售价为700元，一株乙种花木售价为500元。该花农决定在成本不超过29000元的情况下培育甲乙两种花木，若培育乙种花木的株数是甲种花木的3倍还多10株，那么要是总利润不少于18200元，花农有哪几种具体的培育方案？
查看答案和解析>>
科目：初中数学 来源： 题型：
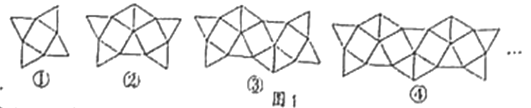
【题目】图1是一组有规律的图案，第①个图集中有4个三角形，第②个图案中有7个三角形，第③个图案中有10个三角形，……依此规律，第⑦个图案中有______个三角形，第n个图案中有______个三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下表：我们把表格中字母的和所得的多项式称为“有特征多项式”，例如：
第1格的“有特征多项式”为，
，
第2格的“有特征多项式”为，
，
回答下列问题：
（1）第3格“有特征多项式”为__________第4格的“有特征多项式”为____________
第
格的“有特征多项式”为__________．
（2）若第
格的“特征多项式”与多项式
的和不含有
项，求此“有特征多项式”．
序号 | 1 | 2 | 3 | 4 | …… |
图形 |
|
|
|
| …… |
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的口袋里装有分别标有汉字“幸”、“福”、“聊”、“城”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．
（1）若从中任取一个球，球上的汉字刚好是“福”的概率为多少？
（2）小颖从中任取一球，记下汉字后放回袋中，然后再从中任取一球，求小颖取出的两个球上汉字恰能组成“幸福”或“聊城”的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图在△ABC中，BO，CO分别平分∠ABC，∠ACB，交于O，CE为外角∠ACD的平分线，BO的延长线交CE于点E，记∠BAC=∠1，∠BEC=∠2，则以下结论①∠1=2∠2，②∠BOC=3∠2，③∠BOC=90°+∠1，④∠BOC=90°+∠2正确的是（ ）
A. ①②③ B. ①③④ C. ①④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
