练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

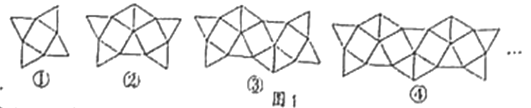
    【题目】图1是一组有规律的图案，第①个图集中有4个三角形，第②个图案中有7个三角形，第③个图案中有10个三角形，……依此规律，第⑦个图案中有______个三角形，第n个图案中有______个三角形．

    【答案】22 (3n+1)

    【解析】

    由题意可知：第（1）个图案有3+1=4个三角形，第（2）个图案有3×2+1=7个三角形，第（3）个图案有3×3+1=10个三角形，…依此规律，第n个图案有（3n+1）个三角形．

    ∵第(1)个图案有3+1=4个三角形，

    第(2)个图案有3×2+1=7个三角形，

    第(3)个图案有3×3+1=10个三角形，

    …

    ∴第n个图案有(3n+1)个三角形.

    当n=7时，

    3n+1=3×7+1=22，

    故答案为：22，(3n+1).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠ACB=90°，D是AB的中点，过点B作∠CBE=∠A，BE与射线CA相交于点E，与射线CD相交于点F．

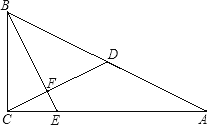
    （1）如图，当点E在线段CA上时，求证：BE⊥CD；

    （2）若BE=CD，那么线段AC与BC之间具有怎样的数量关系？并证明你所得到的结论；

    （3）若△BDF是等腰三角形，求∠A的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

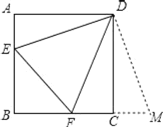
    【题目】如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．若AE=1，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AE是∠BAC的角平分线，交BC于点E，DE∥AB交AC于点D．

    (1)求证AD=ED；

    (2)若AC=AB，DE=3，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

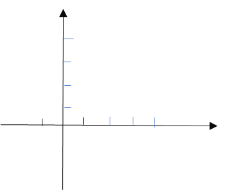
    【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（a，0），（b，0），且满足现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD．

    （1）求点C，D的坐标及四边形ABDC的面积；

    （2）在y轴上是否存在一点M，连接MA，MB，使S△MAB=S四边形ABDC？若存在这样一点，求出点M的坐标；若不存在，试说明理由；

    （3）点P是射线BD上的一个动点（不与B，D重合），连接PC，PA，求∠CPA与∠DCP、∠BAP之间的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

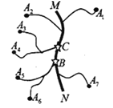
    【题目】如图,在公路 MN 两侧分别有 A, A......A,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是（ ）.

    ①车站的位置设在 C 点好于 B 点;

    ②车站的位置设在 B 点与 C 点之问公路上任何一点效果一样;

    ③车站位置的设置与各段小公路的长度无关.

    A.①B.②C.①③D.②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（规律探索）如图所示的是由相同的小正方形组成的图形，每个图形的小正方形个数为Sn，n是正整数．观察下列图形与等式之间的关系．

    第一组：

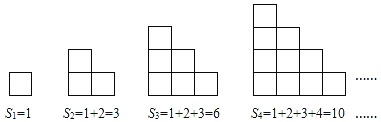
    第二组：

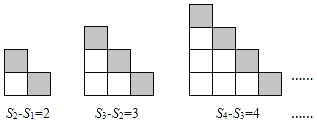
    第三组：

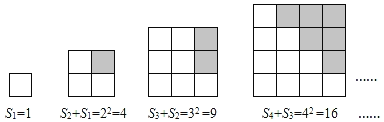
    （规律归纳）

    （1）S7﹣S6＝　 　；Sn﹣Sn﹣1＝　 　．

    （2）S7+S6＝　 　；Sn+Sn﹣1＝　 　．

    （规律应用）

    （3）计算的结果为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（知识生成）我们已经知道，多项式的乘法可以利用图形的面积进行解释．例如利用图1的面积可以得到，基于此，请解答下列问题：

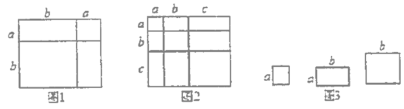
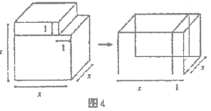
    （1）请你写出图2所表示的一个等式：________．

    （2）小明同学用图3中张边长为的正方形，张边长为的正方形，张宽、长分别为、的长方形纸片拼出一个面积为长方形，则________．

    （知识迁移）（3）事实上，通过计算几何图形的体积也可以表示一些等式，图4表示的是一个边长为的正方体挖去一个小长方体后重新拼成一个新长方体，请你根据图4中图形的变化关系，写出一个代数恒等式：________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为2,.过B作BE//AC.

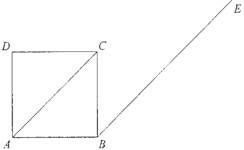
    (1)求BE与AC之间的距离；

    (2)F为BE上一点，连接AF，过C作CG//AF交BE于G.若∠FAB=15°,

    ①依题意补全图形;

    ②求证:四边形AFGC是菱形.

    查看答案和解析>>

    同步练习册答案