
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„A£¨Bµƒ◊¯±Í∑÷±Œ™£®a£¨0£©£¨£®b£¨0£©£¨«“¬˙◊„![]() œ÷Õ¨ ±Ω´µ„A£¨B∑÷±œÚ…œ∆Ω“∆2∏ˆµ•Œª£¨‘ŸœÚ”“∆Ω“∆1∏ˆµ•Œª£¨∑÷±µ√µΩµ„A£¨Bµƒ∂‘”¶µ„C£¨D£¨¡¨Ω”AC£¨BD£Æ
œ÷Õ¨ ±Ω´µ„A£¨B∑÷±œÚ…œ∆Ω“∆2∏ˆµ•Œª£¨‘ŸœÚ”“∆Ω“∆1∏ˆµ•Œª£¨∑÷±µ√µΩµ„A£¨Bµƒ∂‘”¶µ„C£¨D£¨¡¨Ω”AC£¨BD£Æ
£®1£©«Ûµ„C£¨Dµƒ◊¯±Íº∞Àƒ±fl–ŒABDCµƒ√ʪ˝£ª
£®2£©‘⁄y÷·…œ «∑ҥʑ⁄“ªµ„M£¨¡¨Ω”MA£¨MB£¨ πS°˜MAB=SÀƒ±fl–ŒABDC£ø»Ù¥Ê‘⁄’‚—˘“ªµ„£¨«Û≥ˆµ„Mµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨ ‘Àµ√˜¿Ì”…£ª
£®3£©µ„P «…‰œflBD…œµƒ“ª∏ˆ∂ص„£®≤ª”ÎB£¨D÷ÿ∫œ£©£¨¡¨Ω”PC£¨PA£¨«Û°œCPA”ΰœDCP°¢°œBAP÷ƺ‰µƒπÿœµ£Æ
°æ¥∞∏°ø£®1£©C(0£¨2)£¨D(4£¨2)£¨SÀƒ±fl–ŒABDC=8£ª£®2£©M(0£¨4)ªÚ(0£¨-4)£ª£®3£©°œCPA= °œBAP+°œDCPªÚ°œCPA= °œBAP-°œDCP£Æ
°æΩ‚Œˆ°ø
£®1£©”…“‚∏˘æ›∑«∏∫ ˝µƒ–‘÷ «Û≥ˆA°¢B◊¯±Í£¨Ω¯∂¯∑÷Œˆµ√≥ˆC°¢D◊¯±Í£¨ºÃ∂¯º¥ø…«Û≥ˆÀƒ±fl–ŒABDCµƒ√ʪ˝£ª
£®2£©”…“‚ø…÷™“‘ABŒ™µ◊±fl£¨…˵„MµΩABµƒæ‡¿ÎŒ™hº¥»˝Ω«–ŒMABµƒ∏fl£¨«Ûµ√hµƒ÷µº¥ø…µ√≥ˆµ„Mµƒ◊¯±Í£ª
£®3£©∏˘æ›Ã‚“‚∑÷µ±µ„P‘⁄œfl∂ŒBD…œ ±“‘º∞µ±µ„P‘⁄BD—”≥§œfl…œ ±£¨¿˚”√∆Ω––œflµƒ–‘÷ Ω¯––∑÷Œˆº¥ø….
Ω‚: £®1£©”…![]() µ√a=-1£¨b=3£¨‘ÚA(-1£¨0)£¨B(3£¨0)£¨
µ√a=-1£¨b=3£¨‘ÚA(-1£¨0)£¨B(3£¨0)£¨
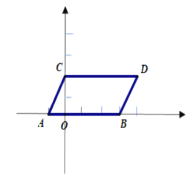
°flµ„A£¨B∑÷±œÚ…œ∆Ω“∆2∏ˆµ•Œª£¨‘ŸœÚ”“∆Ω“∆1∏ˆµ•Œª£¨∑÷±µ√µΩµ„A£¨Bµƒ∂‘”¶µ„C£¨D£¨»ÁÕº£¨
°‡C(0£¨2)£¨D(4£¨2)£¨
°‡SÀƒ±fl–ŒABDC=AB°¡OC=4°¡2=8.
£®2£©¥Ê‘⁄£Æ…˵„MµΩABµƒæ‡¿ÎŒ™h£¨S°˜MAB=![]() °¡AB°¡h=2h£¨
°¡AB°¡h=2h£¨
”…S°˜MAB=SÀƒ±fl–ŒABDC£¨µ√2h=8£¨Ω‚µ√h=4£¨
ø…÷™’‚—˘µƒMµ„‘⁄y÷·…œ”–¡Ω∏ˆ£¨
°‡M(0£¨4)ªÚ(0£¨-4).
£®3£© ¢Ÿµ±µ„P‘⁄œfl∂ŒBD…œ ±£∫°œCPA=°œDCP+°œBAP£¨¿Ì”…»Áœ¬£∫
π˝Pµ„◊˜PE°ŒABΩªOC”ÎEµ„£¨
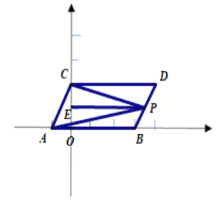
°flAB°ŒCD£¨ PE°ŒAB£¨
°‡AB°ŒPE°ŒCD£¨
°‡°œDCP=°œCPE£¨ °œBAP=°œAPE£¨
°fl°œCPA=°œCPE+°œAPE£¨
°‡°œCPA=°œDCP+°œBAP£ª
¢⁄µ±µ„P‘⁄BD—”≥§œfl…œ ±£∫°œCPA= °œBAP-°œDCP£¨¿Ì”…»Áœ¬£∫
π˝Pµ„◊˜PE°ŒAB£¨

°flAB°ŒCD£¨PE°ŒAB£¨
°‡AB°ŒPE°ŒCD£¨
°‡°œDCP=°œCPE£¨°œBAP=°œAPE£¨
°fl°œCPA= °œAPE-°œCPE°£
°‡°œCPA= °œBAP-°œDCP.


 ≈‡”≈∫√æ̵•‘™º”∆⁄ƒ©æÌœµ¡–¥∞∏
≈‡”≈∫√æ̵•‘™º”∆⁄ƒ©æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®‘ƒ∂¡£©
Œ™¡ÀœÏ”¶°∞—Ùπ‚Ô˝‘À∂Ø°±£¨—ß–£¥Û¡¶ø™’π∏˜œÓÔ˝œÓƒø£¨œ÷ƒ≥÷–—ßÔ˝∂”◊º±∏π∫¬Ú100∏ˆ◊„«Ú∫Õ![]() ∏ˆ¿∫«Ú◊˜Œ™—µ¡∑∆˜≤ƒ£Æœ÷“—÷™”–A£¨B¡Ω∏ˆπ©”¶…Ã∏¯≥ˆ±Íº€»Áœ¬£∫
∏ˆ¿∫«Ú◊˜Œ™—µ¡∑∆˜≤ƒ£Æœ÷“—÷™”–A£¨B¡Ω∏ˆπ©”¶…Ã∏¯≥ˆ±Íº€»Áœ¬£∫
◊„«Ú√ø∏ˆ200‘™£¨¿∫«Ú√ø∏ˆ80‘™£ª
A𩔶…õƒ”≈ª›∑Ω∞∏£∫√ø¬Ú“ª∏ˆ◊„«ÚæÕ‘˘ÀÕ“ª∏ˆ¿∫«Ú£ª
B𩔶…õƒ”≈ª›∑Ω∞∏£∫◊„«Ú°¢¿∫«Úæ˘∞¥∂®º€µƒ80%∏∂øÓ£Æ
£®ÃΩÀ˜£©
£®1£©»Ù![]()
![]() £¨«Îº∆À„ƒƒ÷÷∑Ω∞∏ªÆÀ„£ø
£¨«Îº∆À„ƒƒ÷÷∑Ω∞∏ªÆÀ„£ø
£®2£©![]()
![]() £¨«Î”√∫¨xµƒ¥˙ ˝ Ω£¨∑÷±∞—¡Ω÷÷∑Ω∞∏µƒ∑—”√±Ì æ≥ˆ¿¥£Æ
£¨«Î”√∫¨xµƒ¥˙ ˝ Ω£¨∑÷±∞—¡Ω÷÷∑Ω∞∏µƒ∑—”√±Ì æ≥ˆ¿¥£Æ
£®Õÿ’π£©
£®3£©»Ù![]()
![]() £¨»Áπ˚¡Ω÷÷∑Ω∞∏ø…“‘Õ¨ ± π”√£¨«Î∞Ô÷˙—ß–£…˺∆“ª÷÷◊Ó °«Æµƒ∑Ω∞∏£Æ
£¨»Áπ˚¡Ω÷÷∑Ω∞∏ø…“‘Õ¨ ± π”√£¨«Î∞Ô÷˙—ß–£…˺∆“ª÷÷◊Ó °«Æµƒ∑Ω∞∏£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄°˜ABC∫Õ°˜DEC÷–£¨AC=BC£¨DC=EC£¨°œACB=°œECD=90°„£Æ
£®1£©»ÁÕº1£¨µ±µ„A°¢C°¢D‘⁄Õ¨“ªÃı÷±œfl…œ ±£¨AC=12£¨EC=5£Æ
¢Ÿ«Û÷§£∫AF°ÕBD£¨
¢⁄«ÛAFµƒ≥§∂»£ª
£®2£©»ÁÕº2£¨µ±µ„A°¢C°¢D≤ª‘⁄Õ¨“ªÃı÷±œfl…œ ±£Æ«Û÷§£∫AF°ÕBD£ª
£®3£©»ÁÕº3£¨‘⁄£®2£©µƒÃıº˛œ¬£¨¡¨Ω”CF≤¢—”≥§CFΩªAD”⁄µ„G£¨°œAFG «“ª∏ˆπÃ∂®µƒ÷µ¬£ø»Ù «£¨«Û≥ˆ°œAFGµƒ∂» ˝£¨»Ù≤ª «£¨«ÎÀµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°∞–£‘∞ ÷ª˙°±œ÷œÛ‘Ω¿¥‘Ω ‹µΩ…Áª·µƒπÿ◊¢£Æ°∞∫ƺŸ°±∆⁄º‰£¨ƒ≥–£–°º«’flÀʪ˙µ˜≤È¡Àƒ≥µÿ«¯»Ù∏…√˚—ß…˙∫Õº“≥§∂‘÷–—ß…˙¥¯ ÷ª˙œ÷œÛµƒø¥∑®£¨Õ≥º∆’˚¿Ì≤¢÷∆◊˜¡À»Áœ¬µƒÕ≥º∆Õº£∫

£®1£©«Û’‚¥Œµ˜≤ȵƒº“≥§»À ˝£¨≤¢≤π»´Õº1£ª
£®2£©«ÛÕº2÷–±Ì 溓≥§°∞‘fi≥…°±µƒ‘≤–ƒΩ«µƒ∂» ˝£ª
£®3£©“—÷™ƒ≥µÿ«¯π≤6500√˚º“≥§£¨π¿º∆∆‰÷–∑¥∂‘÷–—ß…˙¥¯ ÷ª˙µƒ¥Û‘º”–∂‡…Ÿ√˚º“≥§£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°˜ABC∫Õ°˜AOD «µ»—¸÷±Ω«»˝Ω«–Œ£¨AB=AC£¨AO=AD£¨°œBAC=°œOAD=90°„£¨µ„O «°˜ABCƒ⁄µƒ“ªµ„£¨°œBOC=130°„£Æ
£®1£©«Û÷§£∫OB=DC£ª
£®2£©«Û°œDCOµƒ¥Û–°£ª
£®3£©…Ë°œAOB=¶¡£¨ƒ«√¥µ±¶¡Œ™∂‡…Ÿ∂» ±£¨°˜COD «µ»—¸»˝Ω«–Œ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
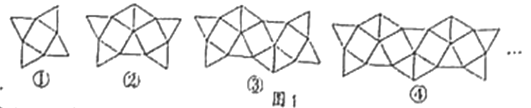
°æƒø°øÕº1 «“ª◊È”–πʬ…µƒÕº∞∏£¨µ⁄¢Ÿ∏ˆÕººØ÷–”–4∏ˆ»˝Ω«–Œ£¨µ⁄¢⁄∏ˆÕº∞∏÷–”–7∏ˆ»˝Ω«–Œ£¨µ⁄¢€∏ˆÕº∞∏÷–”–10∏ˆ»˝Ω«–Œ£¨°≠°≠“¿¥Àπʬ…£¨µ⁄¢fl∏ˆÕº∞∏÷–”–______∏ˆ»˝Ω«–Œ£¨µ⁄n∏ˆÕº∞∏÷–”–______∏ˆ»˝Ω«–Œ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø”–¿Ì ˝a£¨b£¨c‘⁄ ˝÷·…œµƒŒª÷√»ÁÕºÀ˘ 棨«“|a|=|c|£Æ
£®1£©»Ù|a+c|+|b|=2£¨«Ûbµƒ÷µ£ª
£®2£©”√°∞£æ°±¥”¥ÛµΩ–°∞—a£¨b£¨©Åb£¨c¡¨Ω”∆¿¥£Æ
![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
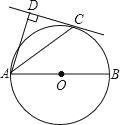
°æƒø°ø»ÁÕº£¨ABŒ™°—Oµƒ÷±æ∂£¨CŒ™°—O…œ“ªµ„£¨AD∫Õπ˝Cµ„µƒ«–œflª•œ‡¥π÷±£¨¥π◊„Œ™D£Æ
£®1£©«Û÷§£∫AC∆Ω∑÷°œDAB£ª
£®2£©π˝µ„O◊˜œfl∂ŒACµƒ¥πœflOE£¨¥π◊„Œ™E£®“™«Û£∫≥flπÊ◊˜Õº£¨±£¡Ù◊˜Õº∫€º££¨≤ª–¥◊˜∑®£©£ª
£®3£©»ÙCD=4£¨AC=4![]() £¨«Û¥πœfl∂ŒOEµƒ≥§£Æ
£¨«Û¥πœfl∂ŒOEµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
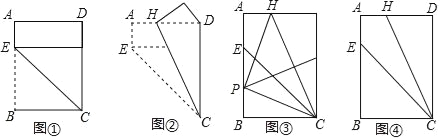
°æƒø°ø∂‘∏¯∂®µƒ“ª’≈æÿ–Œ÷Ω∆¨ABCDΩ¯––»Áœ¬≤Ÿ◊˜£∫œ»—ÿCE’€µ˛£¨ πµ„B¬‰‘⁄CD±fl…œ£®»ÁÕº¢Ÿ£©£¨‘Ÿ—ÿCH’€µ˛£¨’‚ ±∑¢œ÷µ„E«°∫√”ε„D÷ÿ∫œ£®»ÁÕº¢⁄£©
£®1£©∏˘æ›“‘…œ≤Ÿ◊˜∫Õ∑¢œ÷£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©Ω´∏√æÿ–Œ÷Ω∆¨’πø™£Æ
¢Ÿ»ÁÕº¢€£¨’€µ˛∏√æÿ–Œ÷Ω∆¨£¨ πµ„C”ε„H÷ÿ∫œ£¨’€∫€”ÎABœ‡Ωª”⁄µ„P£¨‘ŸΩ´∏√æÿ–Œ÷Ω∆¨’πø™£Æ«Û÷§£∫°œHPC=90°„£ª
¢⁄≤ªΩË÷˙π§æfl£¨¿˚”√Õº¢‹ÃΩÀ˜“ª÷÷–¬µƒ’€µ˛∑Ω∑®£¨’“≥ˆ”ÎÕº¢€÷–Œª÷√œ‡Õ¨µƒPµ„£¨“™«Û÷ª”–“ªÃı’€∫€£¨«“µ„P‘⁄’€∫€…œ£¨«ÎºÚ“™Àµ√˜’€µ˛∑Ω∑®£Æ£®≤ª–ËÀµ√˜¿Ì”…£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com