
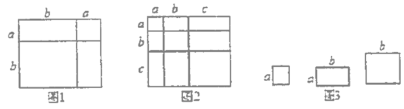
【题目】(知识生成)我们已经知道,多项式的乘法可以利用图形的面积进行解释.例如利用图1的面积可以得到![]() ,基于此,请解答下列问题:
,基于此,请解答下列问题:
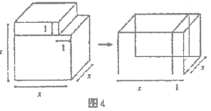
(1)请你写出图2所表示的一个等式:________.
(2)小明同学用图3中![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张宽、长分别为
张宽、长分别为![]() 、
、![]() 的长方形纸片拼出一个面积为
的长方形纸片拼出一个面积为![]() 长方形,则
长方形,则![]() ________.
________.
(知识迁移)(3)事实上,通过计算几何图形的体积也可以表示一些等式,图4表示的是一个边长为![]() 的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:________.
的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:________.
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)9;(3)x3-x=x(x+1)(x-1)
【解析】
(1)依据正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,可得等式;
(2)依据所拼图形的面积为:xa2+yb2+zab,而(2a+b)(a+2b)=2a2+4ab+ab+2b2=2a2+5b2+2ab,即可得到x,y,z的值.
(3)根据原几何体的体积=新几何体的体积,列式可得结论.
解:(1)由图2得:正方形的面积=(a+b+c)2;
正方形的面积=a2+b2+c2+2ab+2ac+2bc;
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)由题意得:(2a+b)(a+2b)=xa2+yb2+zab,
∴2a2+5ab+2b2=xa2+yb2+zab,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ;
;
故答案为:9.
(3)∵原几何体的体积=x3-1×1x=x3-x,新几何体的体积=x(x+1)(x-1),
∴x3-x=x(x+1)(x-1).
故答案为:x3-x=x(x+1)(x-1).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
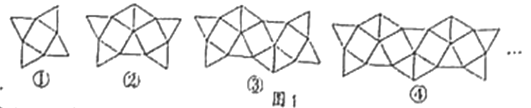
【题目】图1是一组有规律的图案,第①个图集中有4个三角形,第②个图案中有7个三角形,第③个图案中有10个三角形,……依此规律,第⑦个图案中有______个三角形,第n个图案中有______个三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“幸”、“福”、“聊”、“城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“福”的概率为多少?
(2)小颖从中任取一球,记下汉字后放回袋中,然后再从中任取一球,求小颖取出的两个球上汉字恰能组成“幸福”或“聊城”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
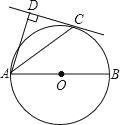
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
(3)若CD=4,AC=4![]() ,求垂线段OE的长.
,求垂线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )

A. ①②③ B. ①③④ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小张某天上午营运全是在东西走向的政府大道上进行的,如果规定向东为正,向西为负,他这天上午的行程是(单位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)将最后一名乘客送达目的地时,小张距上午出发点的距离是多少千米?在出发点的什么方向?
(2)若汽车耗油量为0.6升/千米,出车时,邮箱有油72.2升,若小张将最后一名乘客送达目的地,再返回出发地,问小张今天上午是否需要加油?若要加油至少需要加多少才能返回出发地?若不用加油,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某软件科技公司20人负责研发与维护游戏、网购、视频和送餐共4款软件.投入市场后,游戏软件的利润占这4款软件总利润的40%.如图是这4款软件研发与维护人数的扇形统计图和利润的条形统计图.
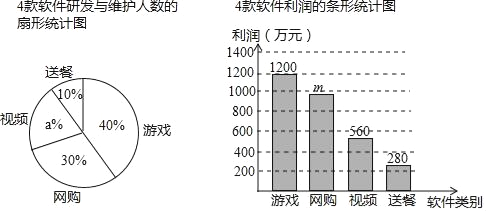
根据以上信息,网答下列问题
(1)直接写出图中a,m的值;
(2)分别求网购与视频软件的人均利润;
(3)在总人数和各款软件人均利润都保持不变的情况下,能否只调整网购与视频软件的研发与维护人数,使总利润增加60万元?如果能,写出调整方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=2![]() ,△ADC与△ABC关于AC所在的直线对称.
,△ADC与△ABC关于AC所在的直线对称.
(1)当OB=2时,求点D的坐标;
(2)若点A和点D在同一个反比例函数的图象上,求OB的长;
(3)如图2,将第(2)题中的四边形ABCD向右平移,记平移后的四边形为A1B1C1D1,过点D1的反比例函数y=![]() (k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
(k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
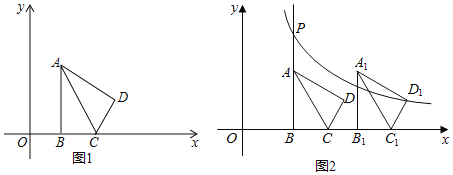
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com