
【题目】某电力维修小组从![]() 点出发,在东西线路上检修电线,如果规定向东为正,向西为负,一天中行驶里程(单位:千米)记录如下:+5,-4,-7,+8,-9,+6,+5
点出发,在东西线路上检修电线,如果规定向东为正,向西为负,一天中行驶里程(单位:千米)记录如下:+5,-4,-7,+8,-9,+6,+5
(1)求收工时在![]() 地的什么方位?
地的什么方位?
(2)在记录中,距离![]() 最远有 千米?
最远有 千米?
(3)若每千米耗油0.2升,油价为5元/升,问出发到收工时共需要多少元油钱?
【答案】(1)东边;(2)7;(3)答:出发到收工时共需要44元油钱.
【解析】
(1)首先把题目的已知数据相加,然后根据结果的正负即可确定收工时在A地的方位;
(2)分别求出每一次距A地的路程即可解答;
(3)首先把所给的数据的绝对值相加,然后乘以0.3再乘以5,即可求解.
解:(1)![]() ,所以收工时在A地的东边;
,所以收工时在A地的东边;
(2)第一次距A地|+5|=5千米;
第二次:|+5-4|=1千米;
第三次:|+5-4-7|=6千米;
第四次:|+5-4-7+8|=2千米;
第五次:|+5-4-7+8-9|=7千米;
第六次:|+5-4-7+8-9+6|=1千米;
第七次:|-+5-4-7+8-9+6+5|=4千米.
所以距A地最远的是7千米,
(3)![]() ,
,
需要的油钱为:44×0.2×5=44(元),
答:出发到收工时共需要44元油钱.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,二次函数y=x2﹣2mx+m2+2m+2的图象与x轴有两个交点.
(1)当m=﹣2时,求二次函数的图象与x轴交点的坐标;
(2)过点P(0,m﹣1)作直线1⊥y轴,二次函数图象的顶点A在直线l与x轴之间(不包含点A在直线l上),求m的范围;
(3)在(2)的条件下,设二次函数图象的对称轴与直线l相交于点B,求△ABO的面积最大时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E.
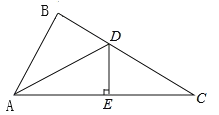
(1)证明∠BAD=∠C;
(2)∠BAD=29°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
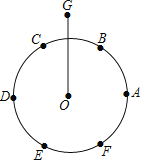
①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;
③连结OG.
问:OG的长是多少?
大臣给出的正确答案应是( )
A. ![]() r B. (1+
r B. (1+![]() )r C. (1+
)r C. (1+![]() )r D.
)r D. ![]() r
r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正两位数的个位数字是a,十位数字比个位数字大2.
(1)列式表示这个两位数;
(2)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新数与原数的和能被22整除.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将矩形纸片![]() 沿对角线
沿对角线![]() 剪开,得到
剪开,得到![]() 和
和![]() .并且量得
.并且量得![]() ,
,![]() .
.
操作发现:
(1)将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,过点
,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 的延长线交于点
的延长线交于点![]() ,则四边形
,则四边形![]() 的形状是________.
的形状是________.
(2)创新小组将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转,使
为旋转中心,按逆时针方向旋转,使![]() 、
、![]() 、
、![]() 三点在同一条直线上,得到如图3所示的
三点在同一条直线上,得到如图3所示的![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,得到四边形
,得到四边形![]() ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将![]() 沿着
沿着![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,此时
重合,此时![]() 点平移至
点平移至![]() 点,
点,![]() 与
与![]() 相交于点
相交于点![]() ,如图4所示,连接
,如图4所示,连接![]() ,试求
,试求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠D=∠C=90°,点E在DC上,且AE,BE分别平分∠BAD和∠ABC.
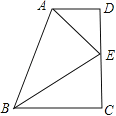
(1)求证:点E为CD中点;
(2)当AD=2,BC=3时,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我市将创建全国森林城市,提出了“共建绿色城”的倡议.某校积极响应,在3月12日植树节这天组织全校学生开展了植树活动,校团委对全校各班的植树情况道行了统计,绘制了如图所示的两个不完整的统计图.
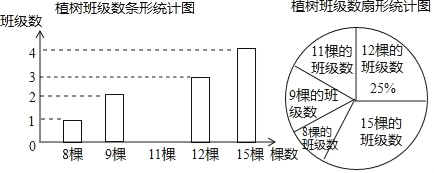
(1)求该校的班级总数;
(2)将条形统计图补充完整;
(3)求该校各班在这一活动中植树的平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com