
【题目】如图,在直角梯形ABCD中,AD∥BC,∠D=∠C=90°,点E在DC上,且AE,BE分别平分∠BAD和∠ABC.
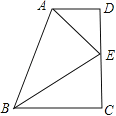
(1)求证:点E为CD中点;
(2)当AD=2,BC=3时,求AB的长.
【答案】(1)见试题解析(2)5.
【解析】
试题(1)过点E作EF⊥AB于F,利用已知条件可证明△ADE≌△AFE,由全等三角形的性质可得DE=FE,同理可证明EF=EC,所以DE=EF=CE,即点E为CD中点;
(2)由(1)可知AF=AD,BC=BF,所以AB=AF+BF=AD+BC=5,问题得解.
试题解析:(1)证明:过点E作EF⊥AB于F,∴∠AFE=90°,∴∠D=∠AFE=90°,∵AE平分∠BAD,
∴∠DAE=∠FAE,在△ADE和△AFE中,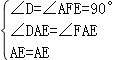 ,∴△ADE≌△AFE(AAS),
,∴△ADE≌△AFE(AAS),
∴DE=FE,同理可得:EF=EC,∴DE=EF=CE,即点E为CD中点;
(2)∵△ADE≌△AFE,∴AF=AD=2,BC=BF=3,∴AB=AF+BF=AD+BC=5.


科目:初中数学 来源: 题型:
【题目】【操作发现】
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B= .
【问题解决】
如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
【灵活运用】
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电力维修小组从![]() 点出发,在东西线路上检修电线,如果规定向东为正,向西为负,一天中行驶里程(单位:千米)记录如下:+5,-4,-7,+8,-9,+6,+5
点出发,在东西线路上检修电线,如果规定向东为正,向西为负,一天中行驶里程(单位:千米)记录如下:+5,-4,-7,+8,-9,+6,+5
(1)求收工时在![]() 地的什么方位?
地的什么方位?
(2)在记录中,距离![]() 最远有 千米?
最远有 千米?
(3)若每千米耗油0.2升,油价为5元/升,问出发到收工时共需要多少元油钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图:已知D为等腰直角△ABC斜边BC上的一个动点(D与B、C均不重合),连结AD,△ADE是等腰直角三角形,DE为斜边,连结CE,求∠ECD的度数.
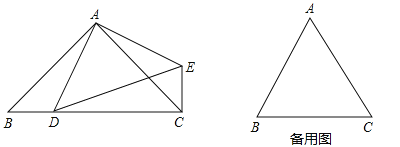
(2)当(1)中△ABC、△ADE都改为等边三角形,D点为△ABC中BC边上的一个动点(D与B、C均不重合),当点D运动到什么位置时,△DCE的周长最小?请探求点D的位置,试说明理由,并求出此时∠EDC的度数.
(3)在(2)的条件下,当点D运动到使△DCE的周长最小时,点M是此时射线AD上的一个动点,以CM为边,在直线CM的下方画等边三角形CMN,若△ABC的边长为4,请直接写出DN长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,连接BF,交边AC于点G,连接CF.
(1)求证:![]() ;
;
(2)如果CF2=FG·FB,求证:CG·CE=BC·DE.
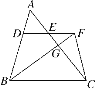
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为( )
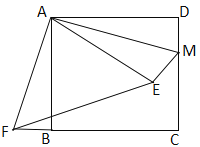
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着航母编队的成立,我国海军日益强大,2018年4月12日,中央军委在南海海域降重举行海上阅兵,在阅兵之前我军加强了海上巡逻,如图,我军巡逻舰在某海域航行到A处时,该舰在观测点P的南偏东45°的方向上,且与观测点P的距离PA为400海里;巡逻舰继续沿正北方向航行一段时间后,到达位于观测点P的北偏东30°方向上的B处,问此时巡逻舰与观测点P的距离PB为多少海里?(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果精确到1海里).
≈1.732,结果精确到1海里).
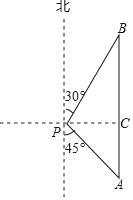
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是正方体的平面展开图,六个面的点数分别为1点、2点、3点、4点、5点、6点,将点数朝外折叠成一枚正方体骰子,并放置于水平桌面上,如图②所示,若骰子初始位置为图②所示的状态,将骰子向右翻滚![]() ,则完成1次翻转,此时骰子朝下一面的点数是2,那么按上述规则连线完成2次翻折后,骰子朝下一面的点数是3点;连续完成2019次翻折后,骰子朝下一面的点数是( )
,则完成1次翻转,此时骰子朝下一面的点数是2,那么按上述规则连线完成2次翻折后,骰子朝下一面的点数是3点;连续完成2019次翻折后,骰子朝下一面的点数是( )
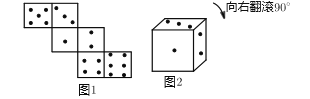
A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com