
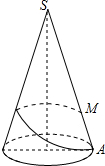
 圆锥的底面半径为10cm,高为10
圆锥的底面半径为10cm,高为10| 5 |
| AO2+SO2 |
| 6 |
| 1 |
| 2 |
| 6 |
| 6 |
| 6 |
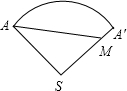 (2)沿母线SA将圆锥的侧面展开,如右图,则线段AM的长就是蚂蚁所走的最短距离
(2)沿母线SA将圆锥的侧面展开,如右图,则线段AM的长就是蚂蚁所走的最短距离| 6 |
nπ×10
| ||
| 180 |
| 6 |


科目:初中数学 来源: 题型:
| A、甲 | B、乙 | C、丙 | D、不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知CD=6米,则旗杆AB的高度为( )
某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知CD=6米,则旗杆AB的高度为( )| A、9米 | ||
B、9(1+
| ||
| C、12米 | ||
| D、18米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
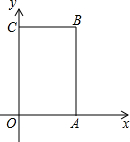 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).查看答案和解析>>
科目:初中数学 来源: 题型:
| A、36,42 |
| B、42,23 |
| C、42,36 |
| D、42,42 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com