
【题目】已知:如图,平行四边形ABCD 中,E、F 两点在对角线 BD 上,BE=DF.
(1) 求证:AE=CF;
(2) 当四边形AECF 为矩形时,直接写出![]()
![]() 的值.
的值.
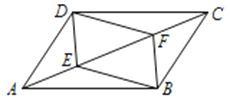
【答案】(1)证明见解析;(2)2.
【解析】(1)证明△ABE≌△CDF,根据全等三角形的对应边相等即可证得;(2)根据四边形AECF为矩形,矩形的对角线相等,则AC=EF,据此即可求解.
解:(1)如图所示,
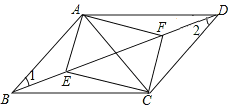
∵ 四边形 ABCD 是平行四边形,
∴AB∥CD,AB=CD,
∴∠1=∠2
在△ABE 和△CDF 中,
AB=CD,∠1=∠2,BE=DF,
∴△ABE≌△CDF(SAS)
∴AE=CF.
(2) 当四边形 AECF 为矩形时, ![]() .
.
“点睛”此类试题属于难度较大的试题,考生解答此类试题时一定要把握好平行四边形的基本性质定理和判定定理,菱形的性质定理和判定定理,矩形的性质定理和判定定理.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】在纪念中国抗日战争胜利70周年之际,某公司决定组织员工观看抗日战争题材的影片,门票有甲乙两种,甲种票比乙种票每张贵6元;买甲种票10张,乙种票15张共用去660元.
(1)求甲、乙两种门票每张各多少元?
(2)如果公司准备购买35张门票且购票费用不超过1000元,那么最多可购买多少张甲种票?
查看答案和解析>>
科目:初中数学 来源: 题型:
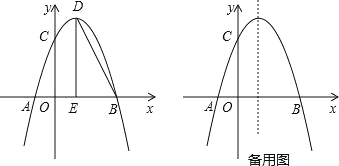
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于点A,点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A,点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在平面内,以线段MN为对角线作正方形MPNQ,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )

A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,4,3分)我市某一周的最高气温统计如下表:
最高气温(℃) | 25 | 26 | 27 | 28 |
天 数 | 1 | 1 | 2 | 3 |
则这组数据的中位数与众数分别是( )
A. 27,28 B. 27.5,28 C. 28,27 D. 26.5,27
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com