Question

【题目】如图，在△ABC中，∠C=90°，AC=BC，∠BAC的平分线AE交BC于点D，且AE⊥BE．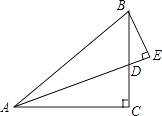
（1）求∠DBE的大小；
（2）求证：AD=2BE．

Answer 1

【答案】
（1）解：∵∠C=90°，AC=BC，

∴∠BAC=45°，

∵AE是∠BAC的平分线，

∴∠CAD= ∠BAC=22.5°，

∵AE⊥BE，

∴∠BED=90°，

∴∠ACD=∠BED=90°，∵∠ADC=∠BDE，

∴∠DBE=∠CAD=22.5°

（2）证明：延长AC、BE交于点G．

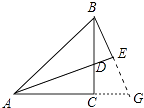
∵AE⊥BG，

∴∠AEB=∠AEG=90°，

在△AEB和△AEG中，

，

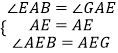∴△AEB≌△AEG，

∴BE=EG，

在△ACD和△BCG中，

，

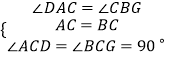∴△ACD≌△BCG，

∴AD=BG=2BE，

∴AD=2BE．

【解析】（1）求出∠CAD，再证明∠DBE=∠CAD即可．（2）先证明△AEB≌△AEG，推出BE=EG，再证明△ACD≌△BCG，推出AD=BG，由此即可证明．
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°．