
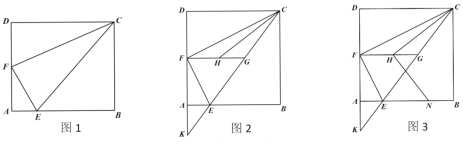
【题目】已知:在矩形ABCD中,点F为AD中点,点E为AB边上一点,连接CE、EF、CF,EF平分∠AEC.
(1)如图1,求证:CF⊥EF;
(2)如图2,延长CE、DA交于点K, 过点F作FG∥AB交CE于点G若,点H为FG上一点,连接CH,若∠CHG=∠BCE, 求证:CH=FK;
(3)如图3, 过点H作HN⊥CH交AB于点N,若EN=11,FH-GH=1,求GK长.
【答案】(1)证明见解析;(2)证明见解析;(3)CN=25.
【解析】
(1)如图,延长EF交CD延长线于点Q,先证明CQ=CE,再证明△FQD≌△FEA,根据全等三角形的对应边相等可得EF=FQ,再根据等腰三角形的性质即可得CF⊥EF;
(2)分别过点F、H作FM⊥CE ,HP⊥CD,垂足分别为M、P,证明四边形DFHP是矩形,继而证明△HPC≌△FMK,根据全等三角形的性质即可得CH=FK;
(3)连接CN,延长HG交CN于点T,设∠DCF=α,则∠GCF=α, 先证明得到FG=CG=GE,∠CGT=2![]() ,再由FG是BC的中垂线,可得BG = CG, ∠CGT=∠FGK=∠BGT=2
,再由FG是BC的中垂线,可得BG = CG, ∠CGT=∠FGK=∠BGT=2![]() ,再证明HN∥BG,得到四边形HGBN是平行四边形,继而证明△HNC≌△KGF,推导可得出HT=CT=TN ,由FH-HG=1,所以设GH=m,则BN=m,FH=m+1,CE=2FG=4m+2,继而根据
,再证明HN∥BG,得到四边形HGBN是平行四边形,继而证明△HNC≌△KGF,推导可得出HT=CT=TN ,由FH-HG=1,所以设GH=m,则BN=m,FH=m+1,CE=2FG=4m+2,继而根据![]() ,可得关于m的方程,解方程求得m的值即可求得答案.
,可得关于m的方程,解方程求得m的值即可求得答案.
(1)如图,延长EF交CD延长线于点Q,

∵矩形ABCD,AB∥CD,
∴∠AEF=∠CQE, ∠A=∠QDF,
又∵EF 平分∠AEC ,
∴∠AEF=∠CEF,
∴∠CEF=∠CQE,
∴CQ=CE,
∵点F是AD中点,
∴AF=DF,
∴△FQD≌△FEA,
∴EF=FQ,
又∵CE=CQ,
∴CF⊥EF;
(2)分别过点F、H作FM⊥CE ,HP⊥CD,垂足分别为M、P,
∵CQ=CE ,CF⊥EF,
∴∠DCF=∠FCE,
又∵FD⊥CD,
∴FM=DF,
∵FG//AB,∴∠DFH=∠DAC=90°,
∴∠DFH=∠FDP=∠DPH=90°,
∴四边形DFHP是矩形,
∴DF=HP,
∴FM= DF=HP,
∵∠CHG=∠BCE,AD∥BC,FG∥CD,
∴∠K=∠BCE=∠CHG=∠DCH,
又∵∠FMK=∠HPC=90°,
∴△HPC≌△FMK,
∴CH=FK;
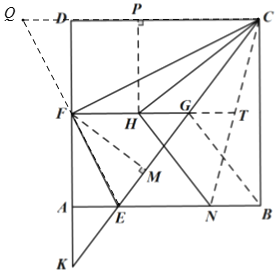
(3)连接CN,延长HG交CN于点T,设∠DCF=α,则∠GCF=α,
∵FG∥CD ,∴∠DCF=∠CFG,
∴∠FCG=∠CFG,∴FG=CG,
∵CF⊥EF,
∴∠FEG+∠FCG=90°,∠CFG+∠GFE=90°,
∴∠GFE=∠FEG,∴GF=FE,
∴FG=CG=GE,∠CGT=2![]() ,
,
∵FG是BC的中垂线,
∴BG = CG, ∠CGT=∠FGK=∠BGT=2![]() ,
,
∵∠CHG=∠BCE=90°-2![]() ,∠CHN=90°,
,∠CHN=90°,
∴∠GHN=∠FGK=∠BGT=2![]() ,
,
∴HN∥BG,
∴四边形HGBN是平行四边形,
∴HG=BN,HN=BG = CG =FG,
∴△HNC≌△KGF,
∴GK=CN,∠HNC=∠FGK=∠NHT=2![]() ,
,
∴HT=CT=TN ,
∵FH-HG=1,∴设GH=m,则BN=m,FH=m+1,CE=2FG=4m+2,
∵GT=![]() ,∴CN=2HT=11+2m,
,∴CN=2HT=11+2m,
∵![]() ,
,
∴![]()
∴![]() (舍去),
(舍去),![]() ,
,
∴CN=GK=2HT=25.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
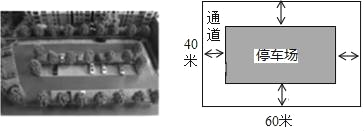
【题目】如图,城市规划部门计划在城市广场的一块长方形空地上修建乙面积为1500m2的停车场,将停车场四周余下的空地修建成同样宽的通道,已知长方形空地的长为60m,宽为40m.
(1)求通道的宽度;
(2)某公司承揽了修建停车场的工程(不考虑修通道),为了尽量减少施工对城市交通的影响,实施施工时,每天的工作效率比原计划增加了20%,结果提前2天完成任务,求该公司原计划每天修建多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
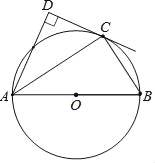
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.
(1)求证:AC平分∠DAB;
(2)求证:AC2=ADAB;
(3)若AD=![]() ,sinB=
,sinB=![]() ,求线段BC的长.
,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是BC边上的点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)如图①,当点E是BC边上任一点(不与点B、C重合)时,求证:AE=EF.
(2)如图②当点E是BC边的延长线上一点时,(1)中的结论还成立吗? (填成立或者不成立).
(3)当点E是BC边上任一点(不与点B、C重合)时,若已知AE=EF,那么∠AEF的度数是否发生变化?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面长18米的墙,用篱笆围成一个矩形场地ABCD,设AD长为x米,AB长为y米,矩形的面积为S平方米.
(1)若篱笆的长为32米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求S与x的函数关系式,并求出使矩形场地的面积为120平方米的围法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,AD=CD,BC=AC,∠BAD=108°,则∠D=( )
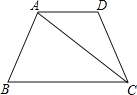
A. 144°B. 110°C. 100°D. 108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的口袋中装有质地、大小相同的小球,甲袋中有2个白球,1个黄球和1个红球:乙袋中装有1个白球,1个黄球和若干个红球,从乙盒中仼意摸取一球为红球的概率是从甲盒中仼意摸取一球为红球的概率的2倍.
(1)乙袋中红球的个数为 .
(2)若摸到白球记1分,摸到黄球记2分,摸到红球记0分,小明从甲、乙两袋中先后分别任意摸取一球,请用树状图或列表的方法求小明摸得两个球得2分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
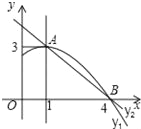
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③b2﹣4ac>0;
④抛物线与x轴的另一个交点是(﹣1,0);
⑤当1<x<4时,有y2<y1;
⑥方程ax2+bx+c=3有两个相等的实数根.
其中正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com