
����Ŀ����ͼ��������y1=ax2+bx+c��a��0��ͼ���һ���֣������ߵĶ�������A��1��3������x���һ������B��4��0����ֱ��y2=mx+n��m��0���������߽���A��B���㣬���н��ۣ�
��2a+b=0��
��abc��0��
��b2��4ac��0��
����������x�����һ�������ǣ���1��0����
�ݵ�1��x��4ʱ����y2��y1��
����ax2+bx+c=3��������ȵ�ʵ������
������ȷ����_____��
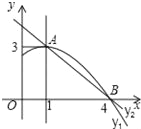
���𰸡��٢ۢݢ���
������������: �����öԳ���x��1�ж���
�ڸ���ͼ��ȷ��a��b��c�ķ��ţ�
�۸�����������x�ύ��ĸ���ȷ����
�ܸ��ݶԳ����жϣ�
����ͼ��ó�����1��x��4ʱ������������ֱ�ߵ����棬��y��y��
����ax2��bx��c��3�ĸ�������ͼ���ϵ�y��3������Ӧ��x��ֵ��
���ϼ��ɵó����ۣ�
���: ����Ϊ�����ߵĶ�������A��1��3�������ԶԳ���Ϊ��x��1����![]() ��1��2a��b��0���ʢ���ȷ��
��1��2a��b��0���ʢ���ȷ��
�ڡ������߿������£�
��a��0��
�߶Գ�����y���Ҳ࣬
��b��0��
����������y�ύ�������ᣬ
��c��0��
��abc��0��
�ʢڲ���ȷ��
�ۡ���������x�����������㣬
��b24ac��0��
�ʢ���ȷ��
����Ϊ�����߶Գ����ǣ�x��1��B��4��0����
������������x�����һ�������ǣ�2��0����
�ʢܲ���ȷ��
����ͼ��ã���1��x��4ʱ����y2��y1���ʢ���ȷ��
�ޡ������ߵĶ�������A��1��3����
���ax2��bx��c��3��������ȵ�ʵ������x��1��
�ʢ���ȷ��
��������ȷ���У��٢ۢݢޣ�
�ʴ�Ϊ���٢ۢݢޣ�
�㾦: ����ѡ��϶࣬�Ƚ����׳��������Ҫ�����������⣬��ȷ���¼����ǹؼ�����ͨ��2a��b��ֵ�������������ߵĶԳ�����ȷ��������������x��Ľ������ȷ�������ֵ����b4ac��ֵ������b4ac��0ʱ����������x����2�����㣻����b4ac��0ʱ����������x����1�����㣻����b4ac��0ʱ����������x��û�н��㣻��֪���Գ���������ߵ�һ�����㣬���öԳ��Կ�������x�����һ���㣮


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���P���߶�AD��һ���㣬OΪBD���е㣬PO���ӳ��߽�BC��Q��
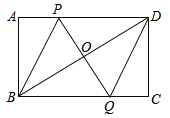
��1����֤���ı���PBQD��ƽ���ı��Σ�
��2����AD��8cm��AB��6cm��P�ӵ�A��������1cm/����ٶ���D�˶�������D�غϣ������P�˶�ʱ��Ϊt�룮
������t��ʾPD�ij�������tΪ��ֵʱ���ı���PBQD�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ھ���ABCD�У���FΪAD�е�,��EΪAB����һ�㣬����CE��EF��CF��EFƽ�֡�AEC.
(1)��ͼ1����֤��CF��EF;
(2)��ͼ2���ӳ�CE��DA���ڵ�K, ����F��FG��AB��CE�ڵ�G������HΪFG��һ�㣬����CH,����CHG=��BCE, ��֤��CH=FK;
(3)��ͼ3, ����H��HN��CH��AB�ڵ�N,��EN=11,FH-GH=1,��GK��.
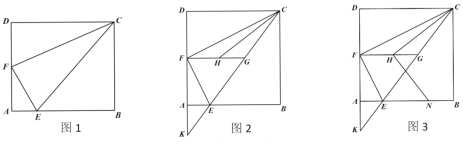
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB�ǡ�O��ֱ������CD��AB��H����CD�ӳ�����һ��E����O�����߽�AB���ӳ�����F���е�ΪG������AG��CD��K��
��1����ͼ1����֤��KE=GE��
��2����ͼ2������CABG������FGB=![]() ��ACH����֤��CA��FE��
��ACH����֤��CA��FE��
��3����ͼ3���ڣ�2���������£�����CG��AB�ڵ�N����sinE=![]() ��AK=
��AK=![]() ����CN�ij���
����CN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() Ϊ
Ϊ![]() �����ȷֵ�.
�����ȷֵ�.

��1����֤![]() ��
��
��2��֤����![]() ��
��
��3������![]() Ϊ�߶�
Ϊ�߶�![]() ��һ���㣬����
��һ���㣬����![]() ��ʹ�߶�
��ʹ�߶�![]() �ij���Ϊ�����ĵ�ĸ���________.��ֱ��д������˵�����ɣ�
�ij���Ϊ�����ĵ�ĸ���________.��ֱ��д������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��AC��AD����ABC�Ľ�ƽ���ߣ�DE��AB��E��DF��AC��F���������ĸ������У���DE��DF����AD������һ�㵽AB��AC�ľ�����ȣ��ۡ�BDE����CDF����BD��CD��AD��BC��������ȷ����(����)
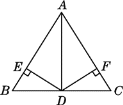
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
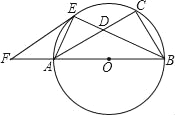
����Ŀ����ͼ����֪��Rt��ABC�ı�ABΪֱ������ABC�����Բ��O����B��ƽ����BE��AC��D������O��E����E��EF��AC��BA���ӳ�����F��
��1����֤��EF�ǡ�O���ߣ�
��2����AB=15��EF=10����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У�AB=2���Ե�AΪԲ�ģ�ABΪ�뾶��Բ����BC�ڵ�E������DE��AC��AE��
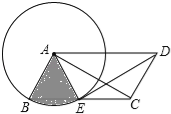
��1����֤����AED�ա�DCA��
��2����DEƽ����ADC������A�����ڵ�E����ͼ����Ӱ���֣����Σ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������a��b��c�������ϵ�λ����ͼ��ʾ��
![]()
(1)�Ƚϴ�С��b____0�� a____c�� b____c�� b��a____0��
(2)A��B�����ľ���Ϊ__________��B��C�����ľ���Ϊ_______��
(3)����|b|��|b��c|��|c��a|��|a��c|��|b��c|.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com