
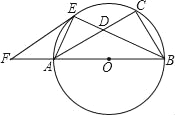
【题目】如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长.
【答案】(1)证明见解析;(2)AE=3![]() .
.
【解析】分析: (1)要证EF是⊙O的切线,只要连接OE,再证∠FEO=90°即可;
(2)证明△FEA∽△FBA,得出AE,BF的比例关系式,勾股定理得出AE,BF的关系式,求出AE的长.
详解:
(1)证明:连接OE,
∵∠B的平分线BE交AC于D,
∴∠CBE=∠ABE.
∵EF∥AC,
∴∠CAE=∠FEA.
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB.
∵∠AEB=90°,
∴∠FEO=90°.
∴EF是⊙O切线.
(2)解:∵AFFB=EFEF,
∴AF×(AF+15)=10×10.
∴AF=5.
∴FB=20.
∵∠F=∠F,∠FEA=∠FBE,
∴△FEA∽△FBE.
∴EF=10
∵AE2+BE2=15×15.
∴AE=3![]() .
.

点睛: 本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.


科目:初中数学 来源: 题型:
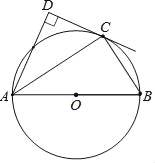
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.
(1)求证:AC平分∠DAB;
(2)求证:AC2=ADAB;
(3)若AD=![]() ,sinB=
,sinB=![]() ,求线段BC的长.
,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的口袋中装有质地、大小相同的小球,甲袋中有2个白球,1个黄球和1个红球:乙袋中装有1个白球,1个黄球和若干个红球,从乙盒中仼意摸取一球为红球的概率是从甲盒中仼意摸取一球为红球的概率的2倍.
(1)乙袋中红球的个数为 .
(2)若摸到白球记1分,摸到黄球记2分,摸到红球记0分,小明从甲、乙两袋中先后分别任意摸取一球,请用树状图或列表的方法求小明摸得两个球得2分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
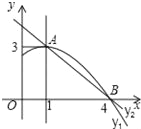
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③b2﹣4ac>0;
④抛物线与x轴的另一个交点是(﹣1,0);
⑤当1<x<4时,有y2<y1;
⑥方程ax2+bx+c=3有两个相等的实数根.
其中正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,正方形 OABC 的边 OA 在数轴上,O 为原点,正方形 OABC 的面积为 16.
(1)数轴上点 A 表示的数为 .
(2)将正方形 OABC 沿数轴水平移动,移动后的正方形记为O' A' B' C' ,移动后的正方形O' A' B' C ' 与原正方形 OABC 重叠部分的面积记为 S,如图 2 中,长方形O ' ABC ' 的面积为 S.当 S 恰好等于原正方形 OABC 面积的![]() 时,数轴上点A' 示的数为 .
时,数轴上点A' 示的数为 .
(3)设点 A 的移动距离AA' = x,D 为线段AA' 的中点,点 E 在线段OO ' 上,且OE = ![]() OO ' ,当OD + OE = 5 时,求x的值并写出此时点 A' 所对应的数.
OO ' ,当OD + OE = 5 时,求x的值并写出此时点 A' 所对应的数.
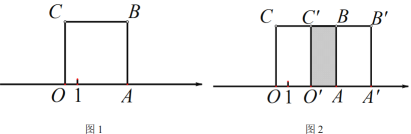
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “明天降雨的概率是60%”表示明天有60%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的概率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的概率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某路公交车从起点出发,经过A、B、C三站到达终点,途中上下乘客如下表所示.(正数表示上车的人数,负数表示下车的人数)
上(下)车 | 起点 | A | B | C | 终点 |
上车的人数 | 10 | 9 | 6 | 5 | 0 |
下车的人数 | 0 | ﹣2 | ﹣5 | ﹣6 | ? |
(1)表格中“?”应填 .
(2)车行驶在哪两站之间时,车上的乘客最多? 站和 站;
(3)若每人乘坐一站需要买票1元,则该车出车一次能收入多少钱?要求写出计算过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一些相同的房间需要粉刷墙面.一天3名一级技工去粉刷8个房间,结果其中有40m2墙面未来得及粉刷;同样时间内5名二级技工刚好粉刷了10个房间,每名一级技工比二级技工一天多粉刷20m2墙面.
(1)一级技工和二级技工每人每天各粉刷多少墙面?
(2)现有若干间这样的房间需要在规定的时间内粉刷完墙面,若安排一名一级技工单独粉刷,可比规定时间提前1天完成;若安排一名二级技工单独完成,到规定时间还有4间房间没粉刷.需要粉刷的房间一共有多少间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com