
����Ŀ����һЩ��ͬ�ķ�����Ҫ��ˢǽ�森һ��3��һ������ȥ��ˢ8�����䣬���������40m2ǽ��δ���ü���ˢ��ͬ��ʱ����5�����������պ÷�ˢ��10�����䣬ÿ��һ�������ȶ�������һ����ˢ20m2ǽ�森
��1��һ�������Ͷ�������ÿ��ÿ�����ˢ����ǽ�棿
��2���������ɼ������ķ�����Ҫ�ڹ涨��ʱ���ڷ�ˢ��ǽ�棬������һ��һ������������ˢ���ɱȹ涨ʱ����ǰ1����ɣ�������һ����������������ɣ����涨ʱ�仹��4�䷿��û��ˢ����Ҫ��ˢ�ķ���һ���ж��ټ䣿
���𰸡���1��100m2ǽ�棻��2��36��
��������
��1����ÿ��һ������ÿ���ˢxm2ǽ�棬��ÿ����������ÿ���ˢ��x��20��m2ǽ�森������ÿ��һ�������ȶ�������һ����ˢ20m2ǽ�����г����̲����
��2������Ҫ��ˢ�ķ���һ����y�䣮������������һ��һ������������ˢ���ɱȹ涨ʱ����ǰ1����ɣ�������һ����������������ɣ����涨ʱ�仹��4�䷿��û��ˢ���г����̲����
�⣺��1����ÿ��һ������ÿ���ˢx m2ǽ�棬��ÿ����������ÿ���ˢ��x��20��m2ǽ�森
�������⣬��![]()
��������̣���x��120��
��x��20��120��20��100 ��m2����
��ÿ��һ������ÿ���ˢ120m2ǽ�棬ÿ����������ÿ���ˢ100m2ǽ�棻
��2������Ҫ��ˢ�ķ���һ����y�䣮
ÿ������ķ�ˢ���Ϊ![]() ��m2��
��m2��
���������֪��![]()
��������̣���y��36��
����Ҫ��ˢ�ķ���һ����36�䣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
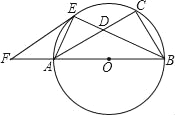
����Ŀ����ͼ����֪��Rt��ABC�ı�ABΪֱ������ABC�����Բ��O����B��ƽ����BE��AC��D������O��E����E��EF��AC��BA���ӳ�����F��
��1����֤��EF�ǡ�O���ߣ�
��2����AB=15��EF=10����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У�AB=AC��D��E��б��BC�����㣬����DAE=45�㣬����ADC�Ƶ�A˳ʱ����ת90��õ���AFB������EF�����н��ۣ�
����AED�ա�AEF��
����ABE�ס�ACD��
��BE+DC=DE��
��BE2+DC2=DE2��
������ȷ���ǣ� ��

A���ڢ� B���٢� C���ڢ� D���٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������a��b��c�������ϵ�λ����ͼ��ʾ��
![]()
(1)�Ƚϴ�С��b____0�� a____c�� b____c�� b��a____0��
(2)A��B�����ľ���Ϊ__________��B��C�����ľ���Ϊ_______��
(3)����|b|��|b��c|��|c��a|��|a��c|��|b��c|.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϣ���A��B��Ӧ�����ֱ�Ϊa��b����a��b����|a+4|+��b��8��2��0��
��1����A��B����ʾ������
��2������C�������϶�Ӧ����Ϊx����x�Ƿ���2x+1��![]() x��8�Ľ⣮
x��8�Ľ⣮
�����߶�BC�ij���
�����������Ƿ���ڵ�P��ʹPA+PB��BC�������ڣ������P��Ӧ�������������ڣ�˵�����ɣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B���߶�CD���������ϣ���A��C��D��B��ʼλ������ʾ�����ֱ�Ϊ-2��0��3��12���߶�CD���������������ÿ��1����λ���ȵ��ٶ��˶����˶�ʱ��Ϊ1��.
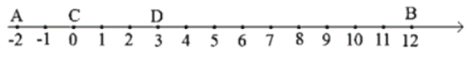
(1)��![]() =0��ʱ��AC�ij�Ϊ________����
=0��ʱ��AC�ij�Ϊ________����![]() =2��ʱ��AC�ij�Ϊ________��
=2��ʱ��AC�ij�Ϊ________��
(2)�ú���![]() �Ĵ���ʽ��ʾAC���߶γ�Ϊ________��
�Ĵ���ʽ��ʾAC���߶γ�Ϊ________��
(3)��![]() =__________��ʱ��AC-BD=5����
=__________��ʱ��AC-BD=5����![]() =___________��ʱAC+BD=15��
=___________��ʱAC+BD=15��
(4)����A���߶�CDͬʱ������������������ƶ�����A���ٶ�Ϊÿ��2����λ���ȣ����ƶ������У��Ƿ����ijһʱ��ʹ��AC=2BD�������ڣ���ֱ�����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��AH�ǡ�O��ֱ����AEƽ�֡�FAH������O�ڵ�E������E��ֱ��FG��AF������ΪF��BΪֱ��OH��һ�㣬��E��F�ֱ��ھ���ABCD�ı�BC��CD�ϣ�
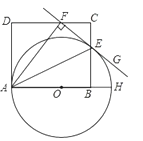
��1����֤��ֱ��FG�ǡ�O�����ߣ�
��2����CD=10��EB=5�����O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ĸ���Ϊm����Ϊn����ͬ�����ΰ���ͼ��ʽƴ��һ�������Σ�
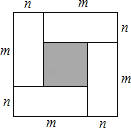
��1������ͼ��д��һ���������ʽ���� ����
��2����֪3m+n��9��mn��6������3m��n��ֵ��
��3����m+n��1����m2+n2����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
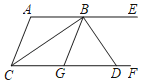
����Ŀ����ͼ��AE��CF����ACF��ƽ���߽�AE�ڵ�B��G��CF�ϵ�һ�㣬��GBE��ƽ���߽�CF�ڵ�D����BD��BC�����н��ۣ���BCƽ�֡�ABG����AC��BG�������DBE����Ľ���2����������A���������BDF��![]() ��������ȷ����_____����������Ϊ��ȷ���۵���Ŷ����ϣ�
��������ȷ����_____����������Ϊ��ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com