
【题目】如图,点A、B和线段CD都在数轴上,点A,C,D,B起始位置所表示的数分别为-2,0,3,12;线段CD沿数轴的正方向以每秒1个单位长度的速度运动,运动时间为1秒.
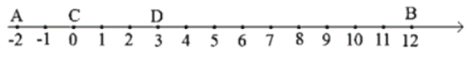
(1)当![]() =0秒时,AC的长为________,当
=0秒时,AC的长为________,当![]() =2秒时,AC的长为________;
=2秒时,AC的长为________;
(2)用含有![]() 的代数式表示AC的线段长为________;
的代数式表示AC的线段长为________;
(3)当![]() =__________秒时,AC-BD=5;当
=__________秒时,AC-BD=5;当![]() =___________秒时AC+BD=15;
=___________秒时AC+BD=15;
(4)若点A与线段CD同时出发沿数轴的正方向移动,点A的速度为每秒2个单位长度,在移动过程中,是否存在某一时刻使得AC=2BD,若存在,请直接求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)2,4;(2)![]() +2;(3)6,11;(4)16秒和
+2;(3)6,11;(4)16秒和![]() 秒
秒
【解析】
(1)依据A、C两点间的距离=|![]() -
-![]() |求解即可;
|求解即可;
(2)![]() 秒后点C运动的距离为
秒后点C运动的距离为![]() 个单位长度,从而点C表示的数;根据A、C两点间的距离=|
个单位长度,从而点C表示的数;根据A、C两点间的距离=|![]() -
-![]() |求解即可.
|求解即可.
(3)1秒后点C运动的距离为![]() 个单位长度,点D运动的距离为
个单位长度,点D运动的距离为![]() 个单位长度,从而可得到点A、点D表示的数;根据两点间的距离=|
个单位长度,从而可得到点A、点D表示的数;根据两点间的距离=|![]() -
-![]() |表示出AC、BD.根据AC-BD=5和AC+BD=15得到关于
|表示出AC、BD.根据AC-BD=5和AC+BD=15得到关于![]() 的含绝对值符号的一元次方程,分别解方程即可得出结论;
的含绝对值符号的一元次方程,分别解方程即可得出结论;
(4)假设能够相等,找出AC、BD,根据AC=2BD即可列出关于![]() 的含绝对值符号的一元一次方程,解方程即可得出结论.
的含绝对值符号的一元一次方程,解方程即可得出结论.
解:(1)当![]() =0秒时,AC=|-2-0|=|-2|=2;
=0秒时,AC=|-2-0|=|-2|=2;
当![]() =2秒时,移动后C表示的数为2,
=2秒时,移动后C表示的数为2,
∴AC=|-2-2|=4.
故答案为:2;4.
(2)点A表示的数为-2,点C表示的数为![]() ;
;
.AC=|-2-![]() |=
|=![]() +2.
+2.
故答案为![]() +2.
+2.
(3)∵![]() 秒后点C运动的距离为
秒后点C运动的距离为![]() 个单位长度,点D运动的距离为
个单位长度,点D运动的距离为![]() 个单位长度.
个单位长度.
∴C表示的数是![]() ,D表示的数是3+
,D表示的数是3+![]() ,
,
∴AC=![]() +2,BD=|12-(3+
+2,BD=|12-(3+![]() )|,
)|,
∵AC-BD=5,
∴![]() +2-|12-(
+2-|12-(![]() +3)|=5,
+3)|=5,
即![]() +2-|9-
+2-|9-![]() |=5,
|=5,
当![]() 时,t+2-(9-t)=5,
时,t+2-(9-t)=5,
解得:![]() =6;
=6;
当t>9时,t+2+(9-t)=5,此时无解;
∴t=6.
∴当![]() =6秒时AC-BD=5;
=6秒时AC-BD=5;
∵AC+BD=15,
∴![]() +2+|12-(
+2+|12-(![]() +3) |=15,
+3) |=15,
即![]() +2+|9-
+2+|9-![]() |=15
|=15
当![]() 时,t+2+(9-t)=15,此时无解;
时,t+2+(9-t)=15,此时无解;
当t>9时,t+2-(9-t)=15,解得t=11;
当![]() =11秒时AC+BD=15,
=11秒时AC+BD=15,
故答案为6,11;
(4)假设能相等,则点A表示的数为2![]() -2,C表示的数为
-2,C表示的数为![]() ,D表示的数为
,D表示的数为![]() +3,B表示的数为12,
+3,B表示的数为12,
∴AC=|2![]() -2-
-2-![]() |=|
|=|![]() -2|,BD=|
-2|,BD=|![]() +3-12|=|
+3-12|=|![]() -9|,
-9|,
∵AC=2BD,
∴|![]() -2|=2|
-2|=2|![]() -9|,
-9|,
∴|![]() -2|=|2
-2|=|2![]() -18|
-18|
解得:![]() =16,
=16,![]() .
.
故在运动的过程中使得AC=2BD,此时运动的时间为16秒和![]() 秒.
秒.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “明天降雨的概率是60%”表示明天有60%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的概率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的概率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OD平分∠BOC,OE平分∠AOC.
(1)若∠BOC=60°,∠AOC=40°,求∠DOE的度数;
(2)若∠DOE=n°,求∠AOB的度数;
(3)若∠DOE+∠AOB=180°,求∠AOB与∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一些相同的房间需要粉刷墙面.一天3名一级技工去粉刷8个房间,结果其中有40m2墙面未来得及粉刷;同样时间内5名二级技工刚好粉刷了10个房间,每名一级技工比二级技工一天多粉刷20m2墙面.
(1)一级技工和二级技工每人每天各粉刷多少墙面?
(2)现有若干间这样的房间需要在规定的时间内粉刷完墙面,若安排一名一级技工单独粉刷,可比规定时间提前1天完成;若安排一名二级技工单独完成,到规定时间还有4间房间没粉刷.需要粉刷的房间一共有多少间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图中网格上按要求画出图形,并回答问题:
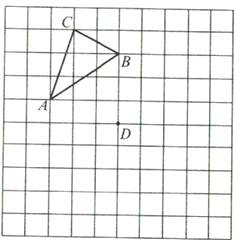
(1)如果将三角形![]() 平移,使得点
平移,使得点![]() 平移到图中点
平移到图中点![]() 位置,点
位置,点![]() 、点
、点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() ,请画出三角形
,请画出三角形![]() ;
;
(2)画出三角形![]() 关于点
关于点![]() 成中心对称的三角形
成中心对称的三角形![]() .
.
(3)三角形![]() 与三角形
与三角形![]() ______(填“是”或“否”)关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点
______(填“是”或“否”)关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的春季趣味运动会深受学生喜爱,该校体育教师为了了解该次运动会中四个项目的受欢迎程度,随机抽取了部分学生进行问卷调查,被调查学生须从“托球跑、掷飞盘、推小车、鸭子步”四个项目中选择自己最喜欢的一项.
根据调查结果,体育教师绘制了图1和图2两个统计图(均未完成),请根据图1和图2的信息,解答下列问题.
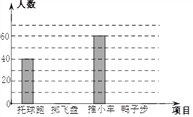
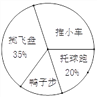
(1)此次共调查了多少名学生?
(2)将条形统计图补充完整.
(3)图2中“鸭子步”所在扇形圆心角为多少度?
(4)若全校有学生1600人,估计该校喜欢“推小车”项目的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图
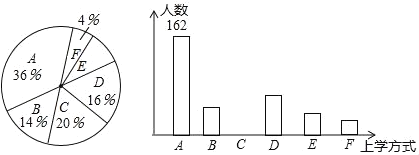
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com