
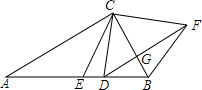
 已知:△ABC中,∠ACB=90°,CE是中线,D是AB上的-点,过D作DF∥AC,过B作BF∥EC,DF、BF相交于F.连结CD、CF,求证:CD=CF.
已知:△ABC中,∠ACB=90°,CE是中线,D是AB上的-点,过D作DF∥AC,过B作BF∥EC,DF、BF相交于F.连结CD、CF,求证:CD=CF. 分析 先根据△ABC中,∠ACB=90°,CE是中线得出AE=CE,故∠A=∠ACE,再由DF∥AC得出∠A=∠BDF,∠ACF+∠DFC=180°,由BF∥EC可知∠CFB+∠ECB=180°,故∠ACE=∠BFD,由此可得出CB是DF的垂直平分线,故可得出结论.
解答 证明:∵△ABC中,∠ACB=90°,CE是中线,
∴AE=CE,
∴∠A=∠ACE.
∵DF∥AC,
∴∠A=∠BDF,∠ACF+∠DFC=180°.
∵BF∥EC,
∴∠CFB+∠ECB=180°,
∴∠ACE=∠BFD,
∴∠BFD=∠BDF,
∴CB是DF的垂直平分线,
∴CD=CF.
点评 本题考查的是直角三角形斜边上的中线,熟知在直角三角形中,斜边上的中线等于斜边的一半是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2=b2+c2+2bccosA | B. | a2=b2+c2+bccosA | ||
| C. | a2=b2+c2-2bccosA | D. | a2=b2+c2-2bcsinA |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小华早晨从家出发匀速步行上学,小华在已步行200米时,爷爷发现小华的眼镜忘在家里,随即出发步行送眼镜去学校.小华到学校后发现眼镜未带上,立即原路返回,途中与爷爷相遇,如图是小华与爷爷之间的距离y米与爷爷出发时间x分钟之间的函数关系图,则小华家到学校的距离为多少米?
小华早晨从家出发匀速步行上学,小华在已步行200米时,爷爷发现小华的眼镜忘在家里,随即出发步行送眼镜去学校.小华到学校后发现眼镜未带上,立即原路返回,途中与爷爷相遇,如图是小华与爷爷之间的距离y米与爷爷出发时间x分钟之间的函数关系图,则小华家到学校的距离为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
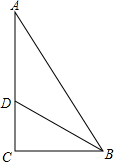 如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=10厘米,BC=8厘米,DC=6厘米,则点D到直线AB的距离是6厘米.
如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=10厘米,BC=8厘米,DC=6厘米,则点D到直线AB的距离是6厘米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com