
分析 设每星期所获利润为y,然后讨论:若销售单价x元,根据一星期利润等于每件的利润×销售量分别得到y=(x-40)[300-10(x-60)](60≤x≤90)或y=(x-40)[300+20(60-x)](0≤x≤20),然后根据获利不得低于40%又不得高于60%求出自变量的取值范围,根据二次函数的性质即可得到答案.
解答 解:∵获利不得低于40%又不得高于60%,
∴$\left\{\begin{array}{l}{x-40≥40%×40}\\{x-40≤60%×40}\end{array}\right.$,
解得:56≤x≤64,
设销售单价为x元时获得的总利润为y元.
涨价时,
y=(x-40)[300-10(x-60)](60≤x≤90)
=(x-40)(900-10x)
=-10x2+1300x-36000
=-10(x2-130x)-36000
=-10(x-65)2+6250,
当60≤x≤64时,x=64,y的最大值是6150,
降价时,
y=(x-40)[300+20(60-x)](40≤x≤60),
=(x-40)(1500-20x)
=-20x2+2300x-60000
=-20(x-57.5)2+6125,
当56≤x≤60时,x=57.5,y的最大值是6125,
综合以上两种情况,定价为64元时可获得最大利润为6150元.
点评 本题主要考查了二次函数的应用,根据题意列出函数表达式是解决问题的关键,根据自变量的取值范围运用函数的性质求最值是本题难点.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
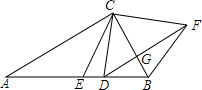 已知:△ABC中,∠ACB=90°,CE是中线,D是AB上的-点,过D作DF∥AC,过B作BF∥EC,DF、BF相交于F.连结CD、CF,求证:CD=CF.
已知:△ABC中,∠ACB=90°,CE是中线,D是AB上的-点,过D作DF∥AC,过B作BF∥EC,DF、BF相交于F.连结CD、CF,求证:CD=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
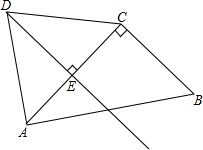 四边形ABCD中,AD=CD,AB=15,AC=12,BC=9,∠ACB=90°.
四边形ABCD中,AD=CD,AB=15,AC=12,BC=9,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 (万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com