
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
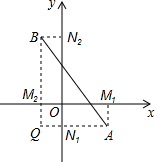 阅读材料:在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离.如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,
阅读材料:在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离.如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,| (x1-x2)2+(y1-y2)2 |
| x2+(y-2)2 |
| (x-3)2+(y-1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| k |
| x |
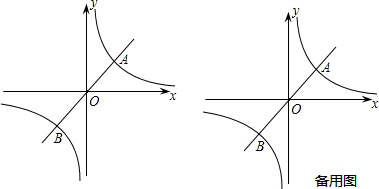
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
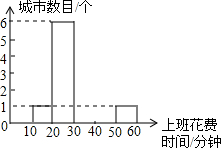 随着我国汽车产业的发展,城市道路拥堵问题日益严峻,某部门对15个城市的交通状况进行了调查,得到的数据如下表所示:
随着我国汽车产业的发展,城市道路拥堵问题日益严峻,某部门对15个城市的交通状况进行了调查,得到的数据如下表所示:| 城市 项目 |
北京 | 太原 | 杭州 | 沈阳 | 广州 | 深圳 | 上海 | 桂林 | 南通 | 海口 | 南京 | 温州 | 威海 | 兰州 | 中山 |
| 上班花费时间(分钟) | 52 | 33 | 34 | 34 | 48 | 46 | 47 | 23 | 24 | 24 | 37 | 25 | 24 | 25 | 18 |
| 上班堵车时间(分钟) | 14 | 12 | 12 | 12 | 12 | 11 | 11 | 7 | 7 | 6 | 6 | 5 | 5 | 5 | 0 |
| 上班堵车时间 |
| 上班花费时间-上班堵车时间 |
| 14 |
| 52-14 |
| 12 |
| 48-12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com