
����Ŀ��Ϊ�˽����꼶ѧ����ѧ�ڲμ����ʵ����������������A�����꼶����ѧ���μ����ʵ��������������ݳ�������������²�������Ƶ���ֲ���������ͳ��ͼ��
A�����꼶����ѧ���μ����ʵ���������Ƶ���ֲ���
���� | Ƶ�� | Ƶ�� |
3 | 20 | 0.10 |
4 | 30 | 0.15 |
5 | 60 | 0.30 |
6 | a | 0.25 |
7 | 40 | 0.20 |
A�����꼶����ѧ���μ����ʵ�������������ͳ��ͼ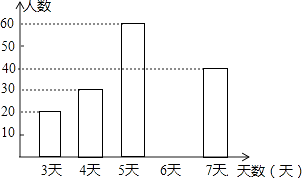
����������Ϣ������������⣻
��1�����Ƶ���ֲ�����a��ֵ������ȫ����ͳ��ͼ��
��2��A�������꼶ѧ��20000�ˣ�������Ƹ������꼶ѧ���μ����ʵ���������5���������
���𰸡�
��1���⣺������ɵã�a=20��01��0.25=50���ˣ�����ͼ��ʾ��
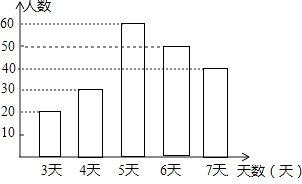
��2���⣺������ɵã�20000����0.30+0.25+0.20��
=15000���ˣ���
�𣺸������꼶ѧ���μ����ʵ���������5�������ԼΪ15000��
��������������Ҫ����������ͳ��ͼ��Ӧ���Լ����������������壬����������������������ǽ���ؼ�����1�����ñ������������������������������Ƶ�����Ƶ�����ɣ��ٲ�ȫ����ͼ����2�����������в�����5���������ռƵ�ʣ��������Ƹ������꼶ѧ���μ����ʵ���������5���������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD����B��C�ġ�O��AD�����ڵ�P����AB��CD�ֱ��ཻ�ڵ�E��F������EF�� 
��1����֤��PFƽ�֡�BFD��
��2����tan��FBC= ![]() ��DF=
��DF= ![]() ����EF�ij���
����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У�AB=AC��AD��BC������Ϊ��D��AN�ǡ�ABC��ǡ�CAM��ƽ���ߣ�CE��AN������Ϊ��E�� 
��1����֤���ı���ADCEΪ���Σ�
��2������ABC����ʲô����ʱ���ı���ADCE��һ�������Σ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y= ![]() x2+x��
x2+x�� ![]() ��
��
��1�����䷽����y= ![]() x2+x��
x2+x�� ![]() ����y=a��x��h��2+k����ʽ��
����y=a��x��h��2+k����ʽ��
��2����ƽ��ֱ������ϵ�У�����������κ�����ͼ��
��3������ͼ����գ�
�ٵ�xʱ��y��x�����������
�ڵ���2��x��2ʱ����y��ȡֵ��Χ����
�۹���x�ķ��� ![]() x2+x��
x2+x�� ![]() =mû��ʵ���⣬��m��ȡֵ��Χ�� ��
=mû��ʵ���⣬��m��ȡֵ��Χ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��С�����ÿ���ʱ��������һ������ܣ�ͼ2�����Ľ���ͼ����ֱ���õ���������ӵĽ���ΪA��B��AB=40cm���������͵�C��AB�ľ���Ϊ10cm���������İ뾶Ϊcm��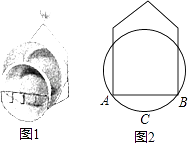
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ƽ���ڵĵ㣬�ֽ��õ�����ƽ��1����λ��������ƽ��2�ĵ�λ�����ֵ���˶���Ϊ��A��бƽ�ƣ����P��2��3����1��бƽ�ƺ�ĵ������Ϊ��3��5������֪��A������Ϊ��1��0����
��1���ֱ�д����A��1�Σ�2��бƽ�ƺ�õ��ĵ�����꣮
��2����ͼ����M��ֱ��l�ϵ�һ�㣬��A���ڵ�M�ĶԳƵ�ĵ�B����B����ֱ��l�ĶԳ���Ϊ��C��
����A��B��C���㲻��ͬһ��ֱ���ϣ��жϡ�ABC�Ƿ���ֱ�������Σ���˵�����ɣ�
������B�ɵ�A��n��бƽ�ƺ�õ����ҵ�C������Ϊ��7��6���������B�����꼰n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ ![]() ������������գ���ɱ���Ľ��
������������գ���ɱ���Ľ��
��1���ⲻ��ʽ�٣�����
��2���ⲻ��ʽ�ڣ�����
��3���Ѳ���ʽ�ٺ͢ڵĽ⼯�������ϱ�ʾ������![]()
��4��ԭ����ʽ��Ľ⼯Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Rt��ABC�У���B=90�㣬AC=20��AB=10��P�DZ�AC��һ�㣨�������˵�A��C��������P��PE��BC�ڵ�E������E��EF��AC����AB�ڵ�F����PC=x��
PE=y��
��1����y��x�ĺ�����ϵʽ��
��2���Ƿ���ڵ�Pʹ��PEF��Rt���������ڣ����ʱ��x��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨����a��b֮���һ�����㣬����(a��b)�����ac��b����ô(a��b)��c.���磺��23��8����(2��8)��3.
(1)���������涨����գ�(3��27)��________��(5��1)��________��![]() ��________��
��________��
(2)С�����о���������ʱ����һ������(3n��4n)��(3��4)��С�����������µ����ɣ�
��(3n��4n)��x����(3n)x��4n����(3x)n��4n��
��3x��4����(3��4)��x��
��(3n��4n)��(3��4)��
���㳢���������ַ����ж�(3��4)��(3��5)��(3��20)�Ƿ����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com