
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E, 
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
【答案】
(1)证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE= ![]() 180°=90°,
180°=90°,
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形
(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
理由:∵AB=AC,
∴∠ACB=∠B=45°,
∵AD⊥BC,
∴∠CAD=∠ACD=45°,
∴DC=AD,
∵四边形ADCE为矩形,
∴矩形ADCE是正方形.
∴当∠BAC=90°时,四边形ADCE是一个正方形
【解析】(1)根据矩形的有三个角是直角的四边形是矩形,已知CE⊥AN,AD⊥BC,所以求证∠DAE=90°,可以证明四边形ADCE为矩形.(2)根据正方形的判定,我们可以假设当AD= ![]() BC,由已知可得,DC=
BC,由已知可得,DC= ![]() BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.
BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,小强和小华共同站在路灯下,小强的身高EF=1.8m,小华的身高MN=1.5m,他们的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且两人相距4.7m,则路灯AD的高度是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△AEC中,∠E=90°,请按如下要求进行操作和判断: 
(1)尺规作图:作△AEC的外接圆⊙O,并标出圆心O(不写画法);
(2)延长CE,在CE的延长线上取点B,使EB=EC,连结AB,设AB与⊙O的交点为D(标出字母B、D),判断:图中 ![]() 与
与 ![]() 相等吗?请说明理由.
相等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是( ) 
A.①②
B.①②③
C.①②④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论正确的有( )
①AD=BD=BC;
②△BCD∽△ABC;
③AD2=ACDC;
④点D是AC的黄金分割点.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=10cm,AD=4cm,作如下折叠操作.如图1和图2所示.在边AB上取点M,在边AD或DC上取点P,连接MP,将△AMP或四边形AMPD沿着直线MP折叠到△A′MP或四边形A′MPD′,点A落点为点A′,点D落点为点D′.
探究:
(1)如图1,若AM=8cm,点P在AD上,点A′落在DC上,则∠MA′C的度数为
(2)如图2,若AM=5cm,点P在DC上,点A′落在DC上.
①求证:△MA′P是等腰三角形;
②请直接写出线段DP的长是
(3)若点M固定为AB的中点,点P由A开始,沿A﹣D﹣C方向,在AD、DC边上运动,设点P的运动速度为1cm/s,运动时间为t s,按操作要求折叠:
①求:当MA′与线段DC有交点时,t的取值范围;
②直接写出当点A′到边AB 的距离最大时,t的值是
发现:若点M在线段AB上移动,点P仍为线段AD或DC上的任意点,随着点M的位置不同,按操作要求折叠后,点A的落点A′的位置会出现以下三种不同的情况:不会落在线段DC上,只有一次落在线段DC上,会有两次落在线段DC上.请直接写出点A′有两次落在线段DC上时,AM的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解七年级学生上学期参加社会实践活动的情况,随机抽查A市七年级部分学生参加社会实践活动天数,并根据抽查结果制作了如下不完整的频数分布表和条形统计图.
A市七年级部分学生参加社会实践活动天数的频数分布表
天数 | 频数 | 频率 |
3 | 20 | 0.10 |
4 | 30 | 0.15 |
5 | 60 | 0.30 |
6 | a | 0.25 |
7 | 40 | 0.20 |
A市七年级部分学生参加社会实践活动天数的条形统计图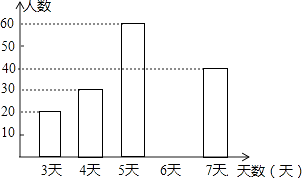
根据以上信息,解答下列问题;
(1)求出频数分布表中a的值,并补全条形统计图.
(2)A市有七年级学生20000人,请你估计该市七年级学生参加社会实践活动不少于5天的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,反比例函数y= ![]() 的图象与一次函数y=k(x﹣2)的图象交点为A(3,2),B(x,y).
的图象与一次函数y=k(x﹣2)的图象交点为A(3,2),B(x,y). 
(1)求反比例函数与一次函数的解析式及B点坐标;
(2)若C是y轴上的点,且满足△ABC的面积为10,求C点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com