
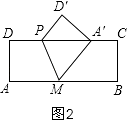
����Ŀ����֪����ABCD�У�AB=10cm��AD=4cm���������۵���������ͼ1��ͼ2��ʾ���ڱ�AB��ȡ��M���ڱ�AD��DC��ȡ��P������MP������AMP���ı���AMPD����ֱ��MP�۵�����A��MP���ı���A��MPD�䣬��A���Ϊ��A�䣬��D���Ϊ��D�䣮
̽����
��1����ͼ1����AM=8cm����P��AD�ϣ���A������DC�ϣ����MA��C�Ķ���Ϊ
��2����ͼ2����AM=5cm����P��DC�ϣ���A������DC�ϣ�
����֤����MA��P�ǵ��������Σ�
����ֱ��д���߶�DP�ij���
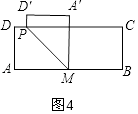
��3������M�̶�ΪAB���е㣬��P��A��ʼ����A��D��C������AD��DC�����˶������P���˶��ٶ�Ϊ1cm/s���˶�ʱ��Ϊt s��������Ҫ���۵���
����MA�����߶�DC�н���ʱ��t��ȡֵ��Χ��
��ֱ��д������A�䵽��AB �ľ������ʱ��t��ֵ��
���֣�����M���߶�AB���ƶ�����P��Ϊ�߶�AD��DC�ϵ�����㣬���ŵ�M��λ�ò�ͬ��������Ҫ���۵���A�����A���λ�û�����������ֲ�ͬ����������������߶�DC�ϣ�ֻ��һ�������߶�DC�ϣ��������������߶�DC�ϣ���ֱ��д����A�������������߶�DC��ʱ��AM��ȡֵ��Χ��
���𰸡�
��1��30��
��2��3cm
��3��5s��4��AM��5.8
���������⣺��1����ͼ1����M��ME��CD��E��
��ME=AD=4��
���۵��ã�AM=A��M=8��
��ME= ![]() A��M��
A��M��
���MA��C=30�㣻
���Դ��ǣ�30�㣻��2������ͼ2�����ı���ABCDΪ���Σ�
��AB��CD��
���CPM=��AMP��
���۵��ã���AMP=��A��MP��
���CPM=��A��MP��
��A��M=A��P��
���MA��P�ǵ��������Σ�����ͼ2�����۵��ã�A��M=AM=5��A��D��=AD=4��
�ɢٵã�A��M=A��P=5��
��Rt��A��PD����PD��= ![]() =3��
=3��
��PD=PD��=3cm��
���Դ��ǣ�3cm����3���ٵ�P��AD�ϣ���A������DC��ʱ����ͼ3��
��M��ME��CD��E��
��M��AB���е㣬AB=10��
��AM=5��
���۵��ã�A��M=AM=5��
��MN=4��
��AP=A��P=xcm��
ͬ���ã�A��E=3��
��A��D=DE��A��E=5��3=2��
PD=4��x��
��Rt��A��DP��x2=22+��4��x��2 ��
���x=2.5��
��ʱ��t=2.5s��
����P��DC�ϣ�A��Ҳ��DC��ʱ����ͼ2��
��ʱPD=3cm��
t=7s��
�൱MA�����߶�DC�н���ʱ��t��ȡֵ��ΧΪ2.5��t��7���ڵ���A�䵽��AB �ľ������ʱ����A��M��ABʱ����ͼ4��
���۵��ã�A��M=AM=5��
��ʱt��ֵ��5s��
���Դ��ǣ�5s��
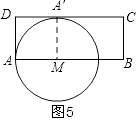
���֣���A�����A�䣬����MΪԲ�ģ�AMΪ�뾶��Բ�ϣ�
��ԲM���߶�CD��Ψһ����ʱ����ͼ5����ʱAM=4cm��
��ԲM���߶�CD�ڵ�Cʱ����ͼ6��
��AM=xcm����CM=xcm��BM=��10��x��cm��
��Rt��MBC�У��ɹ��ɶ����ã�MC2=BM2+BC2 ��
��x2=��10��x��2+42 ��
x=5.8��
���A�������������߶�DC��ʱ��AM��ȡֵ��Χ�ǣ�4cm��AM��5.8cm��
���Դ��ǣ�4cm��AM��5.8cm��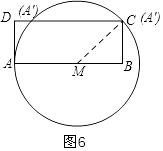
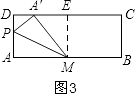
�����㾫�������շ��۱任���۵����⣩�ǽ����ĸ�������Ҫ֪���۵���һ�ֶԳƱ任����������Գƣ��Գ����Ƕ�Ӧ������ߵĴ�ֱƽ���ߣ��۵�ǰ��ͼ�ε���״�ʹ�С���䣬λ�ñ仯����Ӧ�ߺͽ���ȣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��2x+10��x�ᣬy���ཻ��A��B���㣬��C�������ǣ�8��4��������AC��BC��
��1�����O��A��C����������ߵĽ���ʽ�����жϡ�ABC����״��
��2������P�ӵ�O��������OB��ÿ��2����λ���ȵ��ٶ����B�˶���ͬʱ������Q�ӵ�B��������BC��ÿ��1����λ���ȵ��ٶ����C�˶����涨����һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ��PA=QA��
��3���������ߵĶԳ����ϣ��Ƿ���ڵ�M��ʹ��A��B��MΪ������������ǵ��������Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=����x��1��2+5����m��x��n��mn��0ʱ��y����СֵΪ2m�����ֵΪ2n����m+n��ֵΪ�� ��
A.![]()
B.2
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У�AB=AC��AD��BC������Ϊ��D��AN�ǡ�ABC��ǡ�CAM��ƽ���ߣ�CE��AN������Ϊ��E�� 
��1����֤���ı���ADCEΪ���Σ�
��2������ABC����ʲô����ʱ���ı���ADCE��һ�������Σ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��F�ֱ���������ABCD�ı�CD��AD�ϵĵ㣮��CE=DF��AE��BF�ཻ�ڵ�O�����н��ۣ���AE=BF����AE��BF����AO=OE����S��AOB=S�ı���DEOF�У�������� �� ��ֻ����ţ� 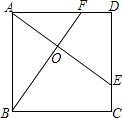
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y= ![]() x2+x��
x2+x�� ![]() ��
��
��1�����䷽����y= ![]() x2+x��
x2+x�� ![]() ����y=a��x��h��2+k����ʽ��
����y=a��x��h��2+k����ʽ��
��2����ƽ��ֱ������ϵ�У�����������κ�����ͼ��
��3������ͼ����գ�
�ٵ�xʱ��y��x�����������
�ڵ���2��x��2ʱ����y��ȡֵ��Χ����
�۹���x�ķ��� ![]() x2+x��
x2+x�� ![]() =mû��ʵ���⣬��m��ȡֵ��Χ�� ��
=mû��ʵ���⣬��m��ȡֵ��Χ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��С�����ÿ���ʱ��������һ������ܣ�ͼ2�����Ľ���ͼ����ֱ���õ���������ӵĽ���ΪA��B��AB=40cm���������͵�C��AB�ľ���Ϊ10cm���������İ뾶Ϊcm��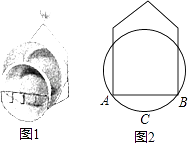
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ ![]() ������������գ���ɱ���Ľ��
������������գ���ɱ���Ľ��
��1���ⲻ��ʽ�٣�����
��2���ⲻ��ʽ�ڣ�����
��3���Ѳ���ʽ�ٺ͢ڵĽ⼯�������ϱ�ʾ������![]()
��4��ԭ����ʽ��Ľ⼯Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C����ABΪֱ���ġ�O�ϣ�AD�����C�����ߴ�ֱ������Ϊ��D��AD����O�ڵ�E��
��1����֤��ACƽ�֡�DAB��
��2������BE��AC�ڵ�F����cos��CAD= ![]() ����
���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com