
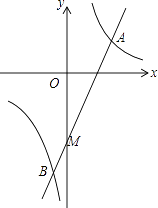
【题目】如图,在平面直角坐标系xOy中,反比例函数y= ![]() 的图象与一次函数y=k(x﹣2)的图象交点为A(3,2),B(x,y).
的图象与一次函数y=k(x﹣2)的图象交点为A(3,2),B(x,y). 
(1)求反比例函数与一次函数的解析式及B点坐标;
(2)若C是y轴上的点,且满足△ABC的面积为10,求C点坐标.
【答案】
(1)解:∵点A(3,2)在反比例函数y= ![]() ,和一次函数y=k(x﹣2)上;
,和一次函数y=k(x﹣2)上;
∴2= ![]() ,2=k(3﹣2),解得m=6,k=2;
,2=k(3﹣2),解得m=6,k=2;
∴反比例函数解析式为y= ![]() ,和一次函数解析式为y=2x﹣4;
,和一次函数解析式为y=2x﹣4;
∵点B是一次函数与反比例函数的另一个交点,
∴ ![]() =2x﹣4,解得x1=3,x2=﹣1;
=2x﹣4,解得x1=3,x2=﹣1;
∴B点的坐标为(﹣1,6)
(2)解:∵点M是一次函数y=2x﹣4与y轴的交点,
∴点M的坐标为(0,﹣4),
设C点的坐标为(0,yc),由题意知 ![]() ×3×|yc﹣(﹣4)|+
×3×|yc﹣(﹣4)|+ ![]() ×1×|yc﹣(﹣4)|=10,
×1×|yc﹣(﹣4)|=10,
解得|yc+4|=5,
当yc+4≥0时,yc+4=5,解得Yc=1,
当yc+4≤0时,yc+4=﹣5,解得Yc=﹣9,
∴点C的坐标为(0,1)或(0,﹣9).
【解析】本题主要考查了反比例函数与一次函数的交点问题,解题的关键是求出两个函数的解析式以及直线AB与y轴的交点坐标,此题难度一般.(1)根据点A(3,2)在反比例函数y= ![]() ,和一次函数y=k(x﹣2)上列出m和k的一元一次方程,求出k和m的值即可;联立两函数解析式,求出交点坐标;(2)设C点的坐标为(0,yc),求出点M的坐标,再根据△ABC的面积为10,知
,和一次函数y=k(x﹣2)上列出m和k的一元一次方程,求出k和m的值即可;联立两函数解析式,求出交点坐标;(2)设C点的坐标为(0,yc),求出点M的坐标,再根据△ABC的面积为10,知 ![]() ×3×|yc﹣(﹣4)|+
×3×|yc﹣(﹣4)|+ ![]() ×1×|yc﹣(﹣4)|=10,求出yC的值即可.
×1×|yc﹣(﹣4)|=10,求出yC的值即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E, 
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式 ![]() ,请结合题意填空,完成本题的解答.
,请结合题意填空,完成本题的解答.
(1)解不等式①,得;
(2)解不等式②,得;
(3)把不等式①和②的解集在数轴上表示出来;![]()
(4)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,
PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内按下列要求完成作图(不要求写作法,保留作图痕迹).
(1)以(0,0)为圆心,3为半径画圆;
(2)以(0,﹣1)为圆心,1为半径向下画半圆;
(3)分别以(﹣1,1),(1,1)为圆心,0.5为半径画圆;
(4)分别以(﹣1,1),(1,1)为圆心,1为半径向上画半圆.
(向上、向下指在经过圆心的水平线的上方和下方)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1)求证:AC平分∠DAB;
(2)连接BE交AC于点F,若cos∠CAD= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a,b之间的一种运算,记作(a,b):如果ac=b,那么(a,b)=c.例如:∵23=8,∴(2,8)=3.
(1)根据上述规定,填空:(3,27)=________,(5,1)=________,![]() =________;
=________;
(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4),小明给出了如下的理由:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n,
∴3x=4,即(3,4)=x,
∴(3n,4n)=(3,4).
请你尝试运用这种方法判断(3,4)+(3,5)=(3,20)是否成立,若成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com