
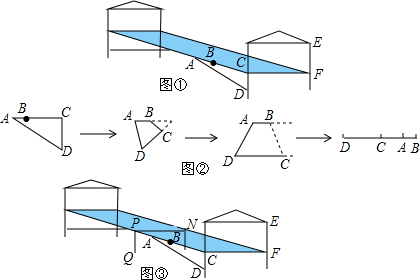
分析 (1)直接利用三角形的稳定性得出答案;
(2)根据已知图形得出AC2+CD2=AD2,以及AB+AD=CD+BC,进而组成方程组求出即可;
(3)先画出床头的示意图,求出BC,OB,再由床腿PQ最大时,床的上方只有圆弧,EF的高度最大时床腿为15cm求解即可.
解答 解:(1)小床这样设计应用的数学原理是:三角形具有稳定性;
故答案为:三角形具有稳定性;
(2)由图2的第一个图形得:AC2+CD2=AD2,
即(6+BC)2+152=AD2①,
又由图2的第三和第四个图形得:AB+AD=CD+BC,
即6+AD=15+BC②,
联立①②组成方程组得:
$\left\{\begin{array}{l}{(6+BC)^{2}+1{5}^{2}=A{D}^{2}}\\{6+AD=15+BC}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{BC=30}\\{AD=39}\end{array}\right.$.
故BC,AD分别取30和39时,才能实现上述变化;
(3)∵如图为床头的示意图,点O为圆心,作OB⊥AD交AD于点B,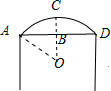
∵AD=80cm,
∴AB=40cm,
∵AO=50cm,
∴BO=$\sqrt{A{O}^{2}-A{B}^{2}}$=$\sqrt{5{0}^{2}-4{0}^{2}}$=30cm,
∴BC=50-30=20cm,
∵床长2m,即200cm,
∴对折后,即床的一半为100cm,
∵床腿PQ最大时,床的上方只有圆弧,
∴2PQ=100-20,解得PQ=40cm,
∵CD=15cm.
∴床头EF的高度最大值为100-2×15-20=50cm.
点评 此题主要考查了几何变换,涉及折叠问题,勾股定理及方程组等知识,解题的关键是能理解折叠图,正确的找出床腿PQ以及床头EF的高度最大时的条件.


科目:初中数学 来源: 题型:选择题
| A. | 了解某班学生的身高情况 | B. | 调查春节晚会的收视率 | ||
| C. | 了解某水库中鱼的种类 | D. | 调查市场上牛奶的质量 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
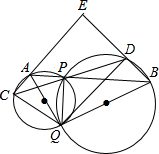 如图所示,两圆O1,O2相交于PQ两点,过P点有两条直线AB、CD,直线AB分别与两圆O1,O2交于点A、B(A、B在P点两侧),直线CD分别与两圆O1,O2交于点C、D(C、D在P点两侧),直线AC与BD交于点E.
如图所示,两圆O1,O2相交于PQ两点,过P点有两条直线AB、CD,直线AB分别与两圆O1,O2交于点A、B(A、B在P点两侧),直线CD分别与两圆O1,O2交于点C、D(C、D在P点两侧),直线AC与BD交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
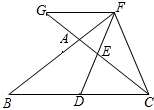 如图,在△ABC中,AB=AC,点D在BC上,点F在BA的延长线上,FD=FC,点E是AC与DF的交点,且ED=EF,FG∥BC交CA的延长线于点G.
如图,在△ABC中,AB=AC,点D在BC上,点F在BA的延长线上,FD=FC,点E是AC与DF的交点,且ED=EF,FG∥BC交CA的延长线于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com