
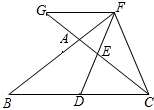
 如图,在△ABC中,AB=AC,点D在BC上,点F在BA的延长线上,FD=FC,点E是AC与DF的交点,且ED=EF,FG∥BC交CA的延长线于点G.
如图,在△ABC中,AB=AC,点D在BC上,点F在BA的延长线上,FD=FC,点E是AC与DF的交点,且ED=EF,FG∥BC交CA的延长线于点G.分析 (1)由AB=AC,可知∠B=∠BCA,由FD=FC,可知∠FDC=∠DCF,根据三角形外角关系和等式性质证明结论;
(2)由FG∥BC,可知∠GFE=∠CDE,根据ASA可证明结论;
(3)先证明∠B=∠G,可根据AAS证明△GFC≌△BDF,则GF=DC,根据△GEF≌△CED,可知GF=CD,等量代换可得结论.
解答 证明:(1)∠BFD=∠GCF,
∵AB=AC,
∴∠B=∠BCA,
∵FD=FC,
∴∠FDC=∠DCF,
∵∠BFD=∠FDC-∠B,
∠GCF=∠DCF-∠BCA,
∴∠BFD=∠GCF;
(2)∵FG∥BC,
∴∠GFE=∠CDE,
在△GEF和△CED中
$\left\{\begin{array}{l}{∠GFE=∠CDE}\\{ED=EF}\\{∠FEG=∠DEC}\end{array}\right.$,
∴△GEF≌△CED
(3)∵FG∥BC
∴∠G=∠BCA
∵∠B=BCA
∴∠B=∠G
在△GFC和△BDF中,
$\left\{\begin{array}{l}{∠B=∠G}\\{∠BFD=∠GCF}\\{FD=FC}\end{array}\right.$,
∴△GFC≌△BDF,
∴GF=BD,
∵△GEF≌△CED,
∴GF=CD,
∴BD=DC.
点评 本题主要考查了全等三角形的判定与性质,熟练的掌握全等三角形的判定方法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
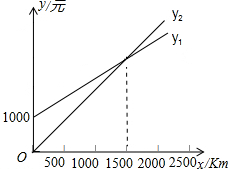 某单位计划与某个体车主或某国营出租车公司中的一家签订月租车合同,设汽车每月行驶x km,应付给个体车主的月租费为y1元,付给出租车公司的月租费为y2元,在同一直角坐标系中y1、y2与x的函数图象如图所示,观察图象回答下列问题:
某单位计划与某个体车主或某国营出租车公司中的一家签订月租车合同,设汽车每月行驶x km,应付给个体车主的月租费为y1元,付给出租车公司的月租费为y2元,在同一直角坐标系中y1、y2与x的函数图象如图所示,观察图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com