
 如图,函数y=-x与函数
如图,函数y=-x与函数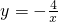 的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D.则四边形ACBD的面积为
的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D.则四边形ACBD的面积为 |k|,得出S△AOC=S△ODB=2,再根据反比例函数的对称性可知:OC=OD,AC=BD,即可求出四边形ACBD的面积.
|k|,得出S△AOC=S△ODB=2,再根据反比例函数的对称性可知:OC=OD,AC=BD,即可求出四边形ACBD的面积.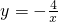 的图象上A,B两点分别作y轴的垂线,垂足分别为点C,D,
的图象上A,B两点分别作y轴的垂线,垂足分别为点C,D, |k|=2,
|k|=2, 中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|;图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|;图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S= |k|,是经常考查的一个知识点;同时考查了反比例函数图象的对称性.
|k|,是经常考查的一个知识点;同时考查了反比例函数图象的对称性. 

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com