
����Ŀ����ͼ���ı���ABCD�Ǿ���ֽƬ��AB=2�����۾���ֽƬABCD��ʹAD��BC�غϣ��ۺ�ΪEF��չƽ���ٹ���B�۵�����ֽƬ��ʹ��A����EF�ϵĵ�N���ۺ�BM��EF�ཻ�ڵ�Q���ٴ�չƽ������BN��MN���ӳ�MN��BC�ڵ�G�������½��ۣ�
�١�ABN=60�㣻��AM=1����QN=![]() ���ܡ�BMG�ǵȱ������Σ���PΪ�߶�BM��һ���㣬H��BN���е㣬��PN+PH����Сֵ��
���ܡ�BMG�ǵȱ������Σ���PΪ�߶�BM��һ���㣬H��BN���е㣬��PN+PH����Сֵ��![]() ��������ȷ���۵������ ��
��������ȷ���۵������ ��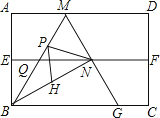
���𰸡��٢ܢ�
���������⣺��ͼ1������AN��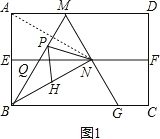
��EF��ֱƽ��AB��
��AN=BN��
�����۵������ʣ��ɵ�
AB=BN��
��AN=AB=BN��
���ABNΪ�ȱ������Σ�
���ABN=60�㣬��PBN=60���2=30�㣬
�����ۢ���ȷ��
�ߡ�ABN=60�㣬��ABM=��NBM��
���ABM=��NBM=60���2=30�㣬
��AM=![]() ��
��
�����ۢڲ���ȷ��
��EF��BC��QN�ǡ�MBG����λ�ߣ�
��QN=![]() BG��
BG��
��BG=BM=![]() ��
��
��QN=![]() ��
��
�����ۢ۲���ȷ��
�ߡ�ABM=��MBN=30�㣬��BNM=��BAM=90�㣬
���BMG=��BNM����MBN=90�㩁30��=60�㣬
���MBG=��ABG����ABM=90�㩁30��=60�㣬
���BGM=180�㩁60�㩁60��=60�㣬
���MBG=��BMG=��BGM=60�㣬
���BMGΪ�ȱ������Σ�
�����ۢ���ȷ��
�ߡ�BMG�ǵȱ������Σ���N��MG���е㣬
��BN��MG����BN=BGsin60��=![]() ��
��
����������֪E���H�����BM�Գƣ���PH=PE��
��P��Q�غ�ʱ��PN+PH��ֵ��С����ʱPN+PH=PN+PE=EN��
��EN=![]() =
=![]() ��
��
��PN+PH=![]() ��
��
��PN+PH����Сֵ��![]() ��
��
�����ۢ���ȷ��
�ʴ�Ϊ���٢ܢݣ�
�����ȸ���EF��ֱƽ��AB���ɵ�AN=BN��Ȼ������۵������ʣ��ɵ�AB=BN���ݴ��жϳ���ABNΪ�ȱ������Σ������жϳ���ABN=60�㣮
�����ȸ��ݡ�ABN=60�㣬��ABM=��NBM�������ABM=��NBM=30�㣻Ȼ����Rt��ABM�У�����AB=2�����AM�Ĵ�С���ɣ�
�����ȸ���EF��BC��QN�ǡ�MBG����λ�ߣ��ɵ�QN=![]() BG��Ȼ�����BG=BM=
BG��Ȼ�����BG=BM=![]() �����QN�ij��ȼ��ɣ�
�����QN�ij��ȼ��ɣ�
�ܸ��ݡ�ABM=��MBN=30�㣬��BNM=��BAM=90�㣬�Ƶá�MBG=��BMG=��BGM=60�㣬�����Ƶá�BMG�ǵȱ������Σ�
�����ȸ��ݡ�BMG�ǵȱ������Σ���N��MG���е㣬�жϳ�BN��MG���������BN�Ĵ�С��Ȼ�����E���H�����BM�ƿɵ�PH=PE�����P��Q�غ�ʱ��PN+PH=PN+PE=EN���ݴ����PN+PH����Сֵ�Ƕ��ټ��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ƥ�˶��������������㶥��������Ķ��������Ĺ�ʽ����ʽ����ʽΪS=a+![]() ��1������ֻ�ǵù�ʽ�е�S��ʾ����ε������a��b����һ����ʾ����α��ϣ������㣩�������������һ����ʾ������ڲ�����������������ǵþ�����a����b��ʾ������ڲ����������������ѡ��һЩ����Ķ���Σ���ͼ1��������֤���õ���ʽ�б�ʾ������ڲ��������������ĸ�� �������������ʽ���ͼ2�ж���ε������ .
��1������ֻ�ǵù�ʽ�е�S��ʾ����ε������a��b����һ����ʾ����α��ϣ������㣩�������������һ����ʾ������ڲ�����������������ǵþ�����a����b��ʾ������ڲ����������������ѡ��һЩ����Ķ���Σ���ͼ1��������֤���õ���ʽ�б�ʾ������ڲ��������������ĸ�� �������������ʽ���ͼ2�ж���ε������ .
�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A1B1A2 �� ��A2B2A3 �� ��A3B3A4 �� ������AnBnAn+1���ǵ���ֱ�������Σ����е�A1��A2������An��x���ϣ���B1��B2������Bn��ֱ��y=x�ϣ���֪OA1=1����OA2015�ij�Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Բ����Ƭ��ֱ�����dzߡ�ֱ�߽�����һ��ƽ���������ϣ���֪��Ƭ��Բ��ΪO�����dzߵ�ֱ�Ƕ���C����ֱ�ߵ�10cm������Ƭ��ֱ�ߵ�Ψһ������A����ֱ�ߵ�14cm������Ƭ�����dzߵ�Ψһ������ΪB������˵��������ǣ�������
A.Բ����Ƭ�İ뾶��4cm
B.�ı���AOBCΪ������
C.��AB�ij���Ϊ4��cm
D.����OAB�������4��cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��B��2m��0����C��3m��0����ƽ��ֱ������ϵ�����㣬����mΪ��������m��0��E��0��n��Ϊy����һ���㣬��BCΪ����x���Ϸ�������ABCD��ʹAB=2BC��������OA���ѡ�ADC�Ƶ�C��ʱ����ת90��á�A��D��C�䣬����ED�䣬������y=ax2+bx+n��a��0����E��A�����㣮
��1����գ���AOB= �㣬��m��ʾ��A������꣺A�䣨 �� ����
��2���������ߵĶ���ΪA�䣬���������߶�AB���ڵ�P����![]() =
=![]() ʱ����D��OE���ABC�Ƿ����ƣ�˵�����ɣ�
ʱ����D��OE���ABC�Ƿ����ƣ�˵�����ɣ�
��3����E��ԭ��O�غϣ�������������OA����һ������Ϊ��M����M��MN��y�ᣬ����ΪN��
����a��b��m����Ĺ�ϵʽ��
�ڵ�mΪ��ֵ�����������ı���ABCD�й����㣬�߶�MN�����ֵΪ10������̽��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����P��BA�ӳ�����һ�㣬PC�С�O�ڵ�C��CG�ǡ�O���ң�CG��AB������ΪD��
��1����֤����PCA=��ABC��
��2������A��AE��PC������O�ڵ�E����CD�ڵ�F������BE����sin��P=![]() ��CF=5����BE�ij���
��CF=5����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������![]() ��ͼ����һ�κ���y=ax+b��ͼ���ཻ�ڵ�A��1��4���͵�B��n����2����
��ͼ����һ�κ���y=ax+b��ͼ���ཻ�ڵ�A��1��4���͵�B��n����2����
��1������������һ�κ����Ľ���ʽ��
��2����һ�κ�����ֵС�ڷ�����������ֵʱ��ֱ��д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��C������A�������������ּƻ���A��C�����м���һ�����ٹ�·�����߶�AC������������ɭ�ֱ�����������P��A���еı�ƫ��60�㷽���ϣ����߶�AC�Ͼ�A����120km��B�����P�ڱ�ƫ��30�㷽���ϣ���֪ɭ�ֱ��������Ե�PΪԲ�ģ�100kmΪ�뾶��Բ���������ʼƻ������������ٹ�·�Ƿ�Խ��������Ϊʲô�����ο����ݣ� ![]() ��1.73��
��1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1�����ھ���ABCD�У�AB=4��BC=3����E������CD�ϵ�һ�����㣬�ѡ�BCE��BE�۵�����C�Ķ�Ӧ��ΪF��
��1������F�պ������߶�AD�Ĵ�ֱƽ������ʱ�����߶�CE�ij���
��2������F�պ������߶�AB�Ĵ�ֱƽ������ʱ�����߶�CE�ij���
��3��������AF���߶�CD�ڵ�Gʱ����ֱ��д��CG�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com