

分析 分别找到图1中图形内的格点数和图形上的格点数后与公式比较后即可发现表示图上的格点数的字母,图2中代入有关数据即可求得图形的面积.
解答 解:根据图1可得,
∵三角形内由1个格点,边上有8个格点,面积为4,即4=1+$\frac{8}{2}$-1;
矩形内由2个格点,边上有10个格点,面积为6,即6=2+$\frac{10}{2}$-1;
∴公式中表示多边形内部整点个数的字母是a;
代入图2中,a=15,b=7,故S=15+$\frac{7}{2}$-1=17.5.
故答案为:17.5
点评 本题考查了图形的变化类问题,解题的关键是能够仔细读题,找到图形内和图形外格点的数目,难度不大.


科目:初中数学 来源: 题型:选择题
 如图,点A、B、C在同一直线上,H为AC的中点,M为AB的中点,N为BC的中点,则下列说法:①MN=HC;②MH=$\frac{1}{2}$(AH-HB);③MN=$\frac{1}{2}$(AC+HB);④HN=$\frac{1}{2}$(HC+HB),其中正确的是( )
如图,点A、B、C在同一直线上,H为AC的中点,M为AB的中点,N为BC的中点,则下列说法:①MN=HC;②MH=$\frac{1}{2}$(AH-HB);③MN=$\frac{1}{2}$(AC+HB);④HN=$\frac{1}{2}$(HC+HB),其中正确的是( )| A. | ①② | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=$\frac{1}{2}$x2-4x+c的顶点为D,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,6),连接BC、CD、BD.
已知抛物线y=$\frac{1}{2}$x2-4x+c的顶点为D,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,6),连接BC、CD、BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处,那么,下列结论中错误的是( )
如图,直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处,那么,下列结论中错误的是( )| A. | AC=DF | B. | ∠DEF=90° | C. | △ABC≌△DEF | D. | EC=CF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
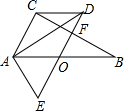 如图,已知Rt△ABC中,∠C=90°,∠B=30°,O为AB边中点,将△ABC绕点O逆时针旋转60°至△EDA位置,连接CD.
如图,已知Rt△ABC中,∠C=90°,∠B=30°,O为AB边中点,将△ABC绕点O逆时针旋转60°至△EDA位置,连接CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com