
����Ŀ��(2016�㶫ʡ÷���е�23��)��Ϊ������⣬���ڴ���ϻ�������Ϊ��Ҫ��ͼ�Σ�
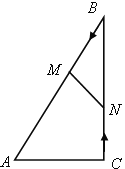
��ͼ����Rt��ABC�У���ACB=90����AC=5cm����BAC=60��������M�ӵ�B��������BA������ÿ��2cm���ٶ����A�����˶���ͬʱ����N�ӵ�C��������CB ������ÿ��![]() cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0
cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0![]() ��������MN��
��������MN��
��1����BM=BN����t��ֵ��
��2������MBN����ABC���ƣ���t��ֵ��
��3����tΪ��ֵʱ���ı���ACNM�������С���������Сֵ��
���𰸡�(1)��10![]() -15��(2)��t=
-15��(2)��t=![]() ��t=
��t=![]() ��(3)��t=2.5����СֵΪ
��(3)��t=2.5����СֵΪ![]()
��������
���������(1)������Rt��ABC�����ʵó�AB��BC�ij��ȣ�Ȼ�����BM=BN�ó�t��ֵ��(2)������MBN�ס�ABC����NBM�ס�ABC��������ֱ����t��ֵ��(3)�������ı��ε����������ABC�������ȥ��BMN������ó���������ʽ���Ӷ������ֵ.
���������(1)������Rt��ABC����ACB=90����AC=5����BAC=60������![]() ��
��![]()
������֪![]() ��
��![]() ��
��![]() �� ��BM=BN��
�� ��BM=BN��![]()
��ã�![]()
(2)��������MBN�ס�ABCʱ�� ��![]() ����
����![]() ����ã�
����ã�![]()
������NBM�ס�ABCʱ�� ��![]() �� ��
�� ��![]() ����ã�
����ã�![]() ��
��
����![]() ��
��![]() ʱ����MBN����ABC������
ʱ����MBN����ABC������
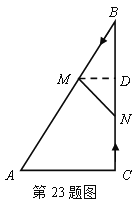
(3)����M��MD��BC�ڵ�D���ɵã�![]() ���ı���ACNM�����Ϊ
���ı���ACNM�����Ϊ![]() ��
��
��![]()
![]()
![]()
![]() ��
��
�����ݶ��κ��������ʿ�֪����![]() ʱ��
ʱ��![]() ��ֵ��С�� ��ʱ��
��ֵ��С�� ��ʱ��![]()


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д� ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������߳��ֱ�Ϊ2��9,�����ߵij�Ϊ���η���x2-14x+48=0��һ��, ����������ε��ܳ�Ϊ( )
A. 11 B. 17 C. 19 D. 17��19
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ����Ķ�������Ϊ��1��4��������ͼ���㣨��2����5������˶��κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����18cm��ϸ��Χ��һ�����������Σ�����һ�߳���8cm������Χ�ɵ��������εĵױ߳�Ϊ______cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
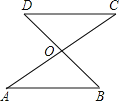
����Ŀ����ͼ���߶�AC��BD���ڵ�D����OA ��OC��������һ��������ʹ��OA B�ա�OCD�����������___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ֱ��y=kx+b������һ�����������ޣ���ֱ��y=bx+k�������������ǣ�������
A.��һ����
B.�ڶ�����
C.��������
D.��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com