
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
①a=40,m=1;
②乙的速度是80km/h;
③甲比乙迟 ![]() h到达B地;
h到达B地;
④乙车行驶 ![]() 小时或
小时或 ![]() 小时,两车恰好相距50km.
小时,两车恰好相距50km.
正确的个数是( )
A.1
B.2
C.3
D.4
【答案】C
【解析】解:①由题意,得m=1.5﹣0.5=1.
120÷(3.5﹣0.5)=40(km/h),则a=40,故①正确;
②120÷(3.5﹣2)=80km/h(千米/小时),故②正确;
③设甲车休息之后行驶路程y(km)与时间x(h)的函数关系式为y=kx+b,由题意,得![]() 解得:
解得: ![]()
∴y=40x﹣20;
根据图形得知:甲、乙两车中先到达B地的是乙车
把y=260代入y=40x﹣20得,x=7,
∵乙车的行驶速度:80km/h;
∴乙车的行驶260km需要260÷80=3.25h,
∴7﹣(2+3.25)= ![]() h.
h.
∴甲比乙迟 ![]() h到达B地,故③正确
h到达B地,故③正确
④当1.5<x≤7时,y=40x﹣20.
设乙车行驶的路程y与时间x之间的解析式为y=k'x+b',由题意得![]()
解得: ![]()
∴y=80x﹣160.
当40x﹣20﹣50=80x﹣160时,
解得:x= ![]() .
.
当40x﹣20+50=80x﹣160时,
解得:x= ![]() .
.
∴ ![]() ﹣2=
﹣2= ![]() ,
, ![]() ﹣2=
﹣2= ![]() .
.
所以乙车行驶小时 ![]() 或
或 ![]() 小时,两车恰好相距50km,故④错误.
小时,两车恰好相距50km,故④错误.
故选(C)


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四个命题中真命题是( )
①三角形有且只有一个内切圆;
②四边形的内角和与外角和相等;
③顺次连接四边形各边中点所得的四边形一定是菱形;
④一组对边平行且一组对角相等的四边形是平行四边形.
A.①②
B.③④
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B 村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
![]()
(2)C村离A村有多远?
(3)若摩托车每100km耗油3升,这趟路共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.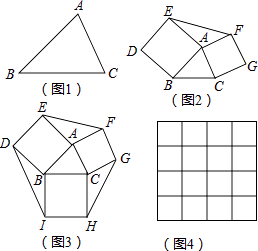
(1)图1中的△ABC的BC边上有一点D,线段AD将△ABC分成两个互补三角形,则点D在BC边的处.
(2)证明:图2中的△ABC分割成两个互补三角形面积相等;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI,已知三个正方形面积分别是17、13、10.则图3中六边形DEFGHI的面积为 . (提示:可先利用图4求出△ABC的面积)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣![]() )=0.
)=0.
(1)判断这个一元二次方程的根的情况;
(2)若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A( ![]() ,0),B(3
,0),B(3 ![]() ,2),C(0,2).动点D以每秒1个单位的速度从点O出发沿OC向终点C运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动.过点E作EF⊥AB,交BC于点F,连接DA、DF.设运动时间为t秒.
,2),C(0,2).动点D以每秒1个单位的速度从点O出发沿OC向终点C运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动.过点E作EF⊥AB,交BC于点F,连接DA、DF.设运动时间为t秒.
(1)求∠ABC的度数;
(2)当t为何值时,AB∥DF;
(3)设四边形AEFD的面积为S.①求S关于t的函数关系式;
②若一抛物线y=﹣x2+mx经过动点E,当S<2 ![]() 时,求m的取值范围(写出答案即可).
时,求m的取值范围(写出答案即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com