
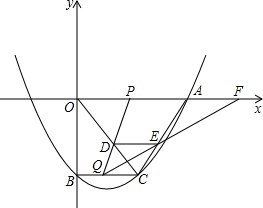
 如图,抛物线y=$\frac{1}{18}{x^2}-\frac{4}{9}$x-10与轴的一个交点为A,与y轴的交点为B.过点B作BC∥x轴,交抛物线于点C,连接AC.动点P、Q分别从0、C两点同时出发,动点P以每秒4个单位的速度沿OA向终点A移动,动点Q以每秒1个单位的速度沿CB向点B移动,当点P停止运动时,点Q也同时停止运动.线段PQ与OC的交点为D,过点D作DE∥x轴,交AC于点E,射线QE交X轴于点F.设点P、Q移动的时间为t(单位:秒).
如图,抛物线y=$\frac{1}{18}{x^2}-\frac{4}{9}$x-10与轴的一个交点为A,与y轴的交点为B.过点B作BC∥x轴,交抛物线于点C,连接AC.动点P、Q分别从0、C两点同时出发,动点P以每秒4个单位的速度沿OA向终点A移动,动点Q以每秒1个单位的速度沿CB向点B移动,当点P停止运动时,点Q也同时停止运动.线段PQ与OC的交点为D,过点D作DE∥x轴,交AC于点E,射线QE交X轴于点F.设点P、Q移动的时间为t(单位:秒).分析 (1)将y=0代入y=$\frac{1}{18}{x^2}-\frac{4}{9}$x-10,求出x的值,得到点A点的坐标;将x=0代入y=$\frac{1}{18}{x^2}-\frac{4}{9}$x-10,求出y的值,得到B点的坐标;
(2)①先由BC∥x轴,DE∥x轴,得出QC∥DE∥PA,根据平行四边形定义可知当PQ∥AC时,四边形CAPQ和四边形CEDQ都是平行四边形,再由平行四边形对边相等得出PA=QC=DE,根据PA=QC列出方程18-4t=t,解方程即可;
②先由QC∥DE∥PA,根据平行线分线段成比例定理得出$\frac{QD}{PD}$=$\frac{CE}{AE}$.由△QDC∽△PDO,△QEC∽△FEA,根据相似三角形对应边成比例得到$\frac{QC}{PO}$=$\frac{QD}{PD}$,$\frac{QC}{FA}$=$\frac{CE}{AE}$,等量代换得出$\frac{QC}{PO}$=$\frac{QC}{FA}$,那么PO=FA,PF=PA+AF=PA+OP=OA=18.再求出C(8,-10),于是BC=8.过Q作QG⊥x轴于点G.在Rt△PQG和Rt△FQG中,利用勾股定理求出PQ2=PG2+GQ2=(4t-8+t)2+102=(5t-8)2+102,FQ2=FG2+GQ2=(18+4t-8+t)2+102=(5t+10)2+102.根据题意求出0<t<$\frac{9}{2}$.然后分三种情况进行讨论:①PQ=PF;②FQ=PF;③PQ=FQ.
解答 解:(1)∵y=$\frac{1}{18}{x^2}-\frac{4}{9}$x-10,
∴当y=0时,$\frac{1}{18}{x^2}-\frac{4}{9}$x-10=0,解得x=18或-10,
当x=0时,y=-10,
∴A(18,0),B(0,-10);
(2)①∵BC∥x轴,DE∥x轴,
∴QC∥DE∥PA,
∴当PQ∥AC时,四边形CAPQ和四边形CEDQ都是平行四边形,此时有PA=QC=DE,
∴当PA=QC时,四边形CEDQ是平行四边形.
∵PA=18-4t,QC=t,
∴18-4t=t,解得t=$\frac{18}{5}$,
∴当四边形CEDQ为平行四边形时,t的值为$\frac{18}{5}$秒;
②∵QC∥DE∥PA,
∴$\frac{QD}{PD}$=$\frac{CE}{AE}$.
∵△QDC∽△PDO,△QEC∽△FEA,
∴$\frac{QC}{PO}$=$\frac{QD}{PD}$,$\frac{QC}{FA}$=$\frac{CE}{AE}$,
∴$\frac{QC}{PO}$=$\frac{QC}{FA}$,
∴PO=FA,
∴PF=PA+AF=PA+OP=OA=18.
令y=-10,得$\frac{1}{18}{x^2}-\frac{4}{9}$x-10=-10,
解得x=8或0,
∴C(8,-10),
∴BC=8.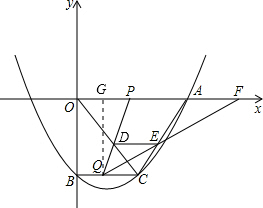 过Q作QG⊥x轴于点G.
过Q作QG⊥x轴于点G.
∵QC=t,PO=4t,PF=18,QG=10,
∴在Rt△PQG和Rt△FQG中,
有PQ2=PG2+GQ2=(4t-8+t)2+102=(5t-8)2+102,
FQ2=FG2+GQ2=(18+4t-8+t)2+102=(5t+10)2+102.
∵动点P、Q分别从0、C两点同时出发,动点P以每秒4个单位的速度沿OA向终点A移动,动点Q以每秒1个单位的速度沿CB向点B移动,当点P停止运动时,点Q也同时停止运动,
∴4t<18,
解得t<$\frac{9}{2}$,
∴0<t<$\frac{9}{2}$.
①若PQ=PF,则(5t-8)2+102=182,
解得t=$\frac{8+4\sqrt{14}}{5}$>$\frac{9}{2}$,或t=$\frac{8-4\sqrt{14}}{5}$<0,都不符合题意,舍去;
②若FQ=PF,则(5t+10)2+102=182,
解得t=$\frac{-10+4\sqrt{14}}{5}$,符合题意;或t=$\frac{-10-4\sqrt{14}}{5}$<0,不符合题意,舍去;
③若PQ=FQ,则(5t-8)2+102=(5t+10)2+102,
解得t=-$\frac{1}{5}$<0,不符合题意,舍去;
综上所述,当△PQF为等腰三角形时,t的值为$\frac{-10+4\sqrt{14}}{5}$秒.
点评 本题是二次函数的综合题型,其中涉及到的知识点有二次函数图象上点的坐标特征,平行四边形的判定与性质,平行线分线段成比例定理,相似三角形的判定与性质,等腰三角形的性质,勾股定理.在求有关动点问题时要注意分析题意分情况讨论结果.


科目:初中数学 来源: 题型:解答题
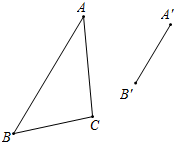 如图,已知△ABC和△A′B′C′是位似比为2的位似三角形,且AB的对应边是A′B′,请用尺规作图,将△A′B′C′补充完整(可不写作法,但保留作图痕迹).
如图,已知△ABC和△A′B′C′是位似比为2的位似三角形,且AB的对应边是A′B′,请用尺规作图,将△A′B′C′补充完整(可不写作法,但保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
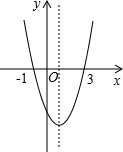 二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①bc<0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③4a-2b+c>0;④当x>0时,y随x值的增大而增大;⑤当y>0时,-1<x<3.其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①bc<0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③4a-2b+c>0;④当x>0时,y随x值的增大而增大;⑤当y>0时,-1<x<3.其中正确的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
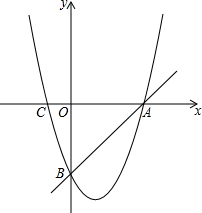 如图,抛物线y=x2-2x+n与直线y=x-3相交于A、B两点(点A在x轴上,点B在y轴上),与x轴的另一个交点为点C.
如图,抛物线y=x2-2x+n与直线y=x-3相交于A、B两点(点A在x轴上,点B在y轴上),与x轴的另一个交点为点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1•y2<0 | B. | y1+y2<0 | C. | y1-y2>0 | D. | y1-y2<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com