
分析 由二次根式的性质可得1≤x≤2,然后由柯西不等式求得y=2$\sqrt{x-1}$+$\sqrt{2-x}$≤$\sqrt{{1}^{2}+{2}^{2}}$•$\sqrt{(\sqrt{x-1})^{2}+(\sqrt{2-x})^{2}}$=$\sqrt{5}$×$\sqrt{x-1+2-x}$=$\sqrt{5}$.
解答 解:根据题意得:$\left\{\begin{array}{l}{x-1≥0}\\{2-x≥0}\end{array}\right.$,
解得:1≤x≤2,
由柯西不等式得:y=2$\sqrt{x-1}$+$\sqrt{2-x}$
≤$\sqrt{{1}^{2}+{2}^{2}}$•$\sqrt{(\sqrt{x-1})^{2}+(\sqrt{2-x})^{2}}$
=$\sqrt{5}$×$\sqrt{x-1+2-x}$
=$\sqrt{5}$(当且仅当2$\sqrt{2-x}$=$\sqrt{x-1}$,即x=$\frac{9}{5}$时,取等号),
故函数y=2$\sqrt{x-1}$+$\sqrt{2-x}$的最大值为$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 此题考查了无理函数的最值问题.此题难度适中,注意掌握柯西不等式的应用是解此题的关键,注意柯西不等式:ax+by≤$\sqrt{{a}^{2}+{b}^{2}}$•$\sqrt{{x}^{2}+{y}^{2}}$(当且仅当ay=bx时取“=”).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
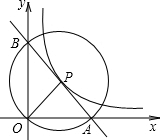 如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=$\frac{k}{x}$(x>0)的图象上任意一点,以P为圆心,PO为半径的圆与x轴、y轴分别交于点A、B.
如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=$\frac{k}{x}$(x>0)的图象上任意一点,以P为圆心,PO为半径的圆与x轴、y轴分别交于点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
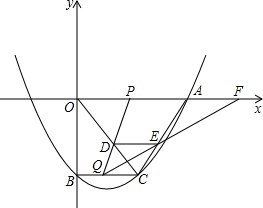 如图,抛物线y=$\frac{1}{18}{x^2}-\frac{4}{9}$x-10与轴的一个交点为A,与y轴的交点为B.过点B作BC∥x轴,交抛物线于点C,连接AC.动点P、Q分别从0、C两点同时出发,动点P以每秒4个单位的速度沿OA向终点A移动,动点Q以每秒1个单位的速度沿CB向点B移动,当点P停止运动时,点Q也同时停止运动.线段PQ与OC的交点为D,过点D作DE∥x轴,交AC于点E,射线QE交X轴于点F.设点P、Q移动的时间为t(单位:秒).
如图,抛物线y=$\frac{1}{18}{x^2}-\frac{4}{9}$x-10与轴的一个交点为A,与y轴的交点为B.过点B作BC∥x轴,交抛物线于点C,连接AC.动点P、Q分别从0、C两点同时出发,动点P以每秒4个单位的速度沿OA向终点A移动,动点Q以每秒1个单位的速度沿CB向点B移动,当点P停止运动时,点Q也同时停止运动.线段PQ与OC的交点为D,过点D作DE∥x轴,交AC于点E,射线QE交X轴于点F.设点P、Q移动的时间为t(单位:秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | DA=D′A′ | B. | ∠B=∠B′ | C. | ∠B=∠B′,∠C=∠C′ | D. | ∠B=∠B′,∠D=∠D′ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com